Законы Кеплера

Законы Кеплера о движении планет, сформулированные немецким математиком и астрономом Иоганном Кеплером в начале XVII века, произвели революцию в нашем понимании движения небесных тел, особенно планет, вращающихся вокруг Солнца. Эти законы послужили прочным фундаментом для последующей работы Исаака Ньютона о всемирном тяготении и заложили основу для современной небесной механики. Открытия Кеплера стали большим скачком вперед в области астрономии и существенно повлияли на наше понимание структуры и поведения Солнечной системы.

История вопроса

Иоганн Кеплер (1571-1630) был ключевой фигурой научной революции, преодолев разрыв между работами Коперника и Галилея и проложив путь к новаторским законам движения Ньютона. Кеплер родился в Вайль-дер-Штадте, Германия, и сначала получил образование теолога, но вскоре у него появился интерес к астрономии. Он стал помощником датского астронома Тихо Браге и использовал обширные данные наблюдений Браге для разработки своих законов движения планет.

Первый закон Кеплера: Закон эллипсов

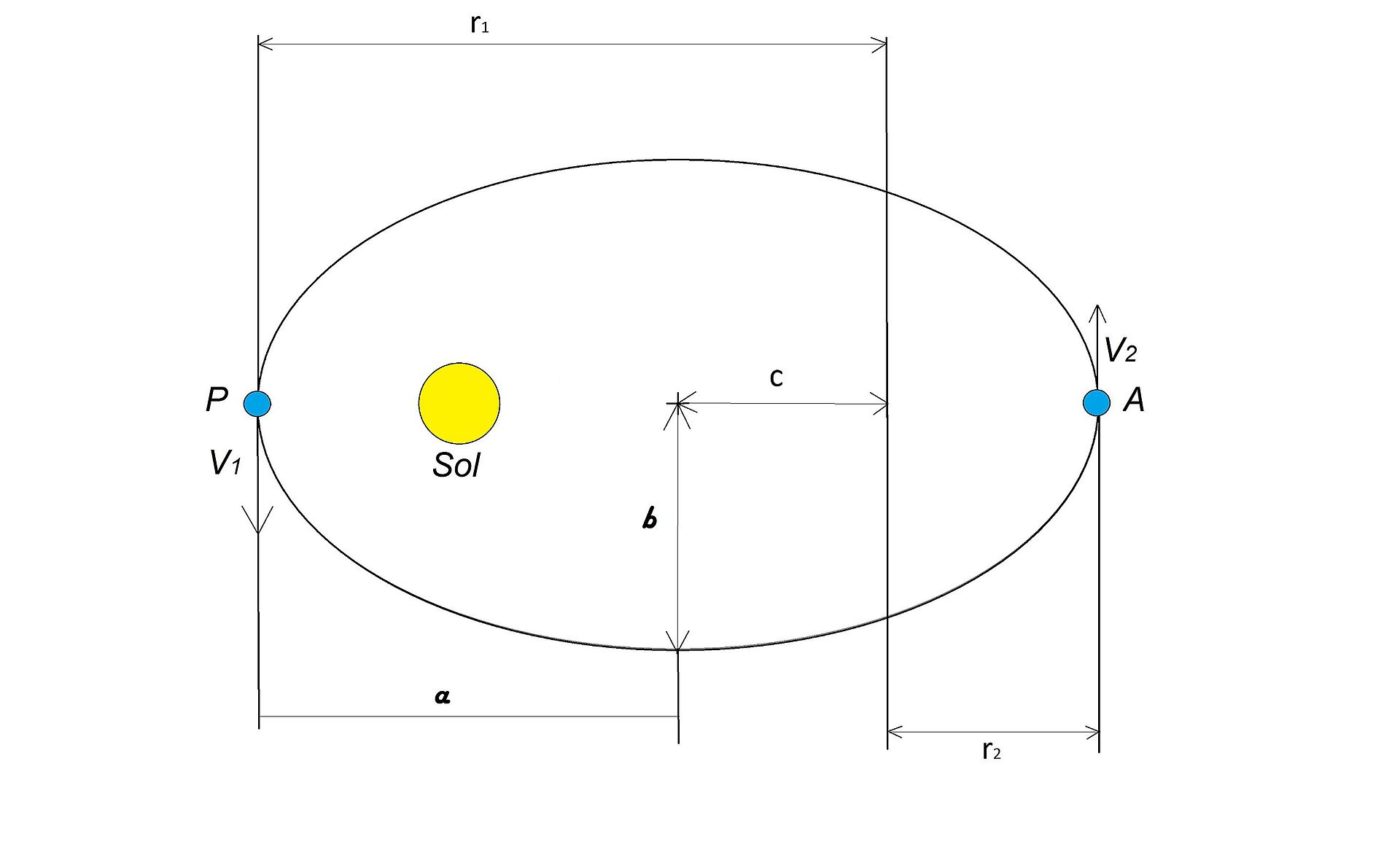
Первый закон Кеплера, также известный как закон эллипсов, гласит, что орбита каждой планеты вокруг Солнца представляет собой эллипс с Солнцем в одном из двух центров. Эллипс - это геометрическая фигура, напоминающая вытянутый круг с двумя точками, называемыми фокусами (множественное число от "фокус"). Солнце находится в одном из этих фокусов, а планета движется по эллиптической траектории с Солнцем в центре ее притяжения. Этот закон противоречил более раннему убеждению, что планеты движутся по идеальным кругам вокруг Земли.

Эксцентриситет эллипса определяет его форму: от идеально круглой орбиты (эксцентриситет равен 0) до сильно вытянутой орбиты (эксцентриситет близок к 1). Первый закон Кеплера подразумевает, что эксцентриситет орбиты планеты связан с ее расстоянием от Солнца. Планеты с низким эксцентриситетом, такие как Земля, имеют почти круговые орбиты, а планеты с более высоким эксцентриситетом, такие как кометы, имеют более вытянутые орбиты.

Второй закон Кеплера: Закон площадей

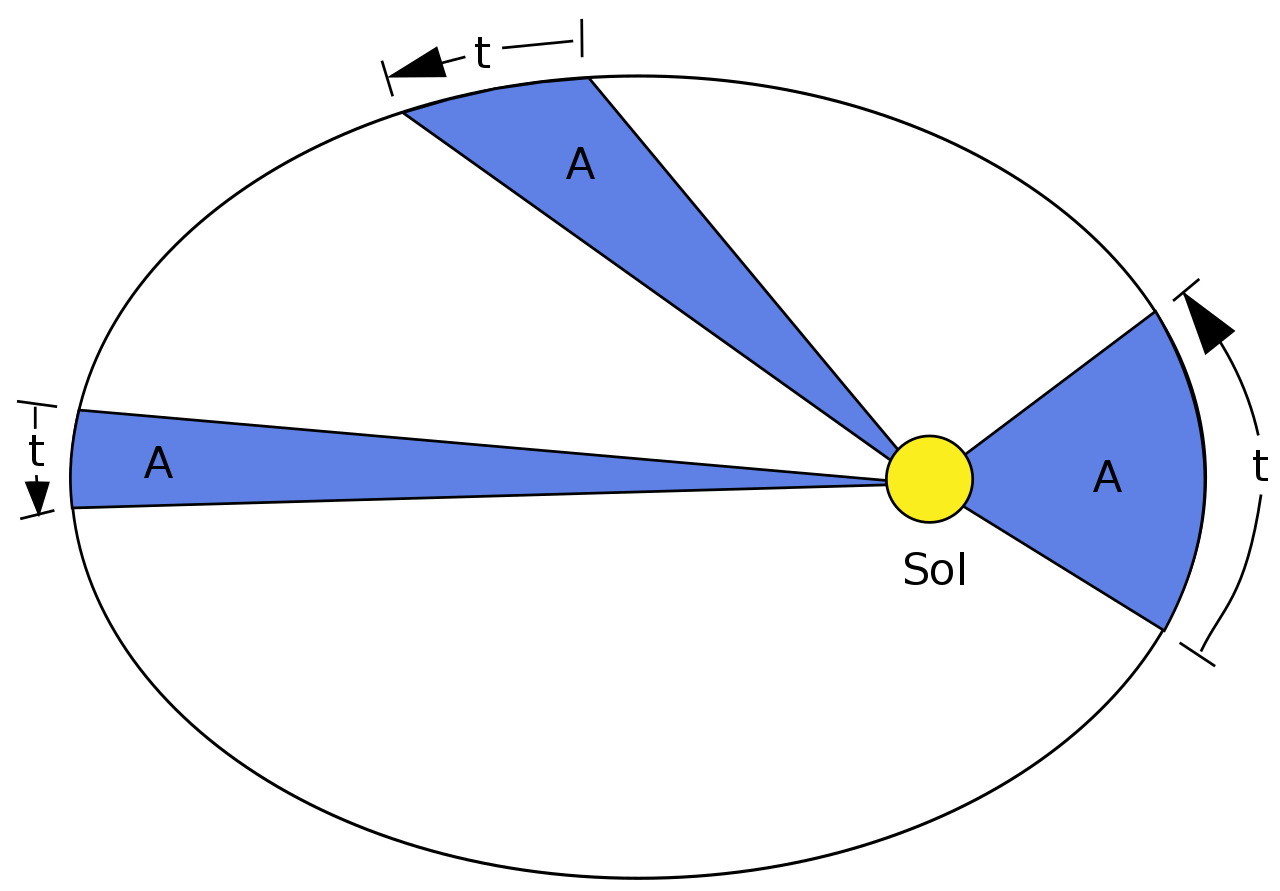
Второй закон Кеплера, часто называемый законом площадей, описывает скорость, с которой планета движется по своей орбите. Он гласит, что линия, соединяющая планету с Солнцем, проходит равные участки за равные промежутки времени. Проще говоря, когда планета находится ближе к Солнцу (в перигелии), она движется быстрее, а когда дальше (в афелии), то медленнее.

Этот закон имеет важные последствия для понимания сохранения углового момента. Когда планета движется ближе к Солнцу, ее скорость увеличивается, чтобы сохранить угловой момент, а когда она удаляется, скорость уменьшается. Таким образом, планета проводит больше времени во внешних частях своей орбиты, в результате чего за равные промежутки времени проходит равные площади.

Третий закон Кеплера: Гармонический закон

Третий закон Кеплера, часто называемый гармоническим законом, устанавливает математическую зависимость между орбитальным периодом планеты и ее средним расстоянием от Солнца. Он гласит, что квадрат орбитального периода планеты прямо пропорционален кубу ее среднего расстояния от Солнца. Математически это можно выразить следующим образом:

Т² = к × R³

Где:

• T - орбитальный период планеты (в годах),
• R - среднее расстояние от планеты до Солнца (в астрономических единицах), и
• k - константа пропорциональности, которая зависит от масс соответствующих объектов.

Этот закон позволяет астрономам рассчитать период обращения планеты на основе ее среднего расстояния от Солнца и наоборот. Кроме того, это послужило важной ступенькой для более поздней работы Ньютона по универсальному тяготению и пониманию того, что сила, управляющая движением планет, связана с их массами и расстоянием от Солнца.

Наследие и влияние

Законы Кеплера о движении планет ознаменовали собой значительный поворот в научной мысли и заложили основу для будущих достижений в области астрономии и физики. Эти законы продемонстрировали, что движение планет можно описать математически, и позволили по-новому взглянуть на фундаментальные принципы, определяющие движение небесных тел.

Основываясь на законах Кеплера, Исаак Ньютон включил их в свои законы движения и всемирного тяготения. Работа Ньютона, опубликованная в его монументальном труде "Philosophiæ Naturalis Principia Mathematica" в 1687 году, дала исчерпывающее объяснение движения небесных тел и создала единую основу для понимания физических законов, управляющих Вселенной.

Сегодня законы Кеплера остаются основополагающими принципами в области астрономии и небесной механики. Они преподаются в учебных заведениях по всему миру и служат основой для точного предсказания положения планет, изучения экзопланет и исследования нашей собственной Солнечной системы.

Законы Кеплера о движении планет представляют собой поворотный момент в истории науки, освещая природу нашей Солнечной системы и способствуя пониманию человечеством космоса. Они свидетельствуют о силе наблюдения, математического мышления и неустанного стремления к знаниям, которые двигают научный прогресс.