Всегда ли прямая линия - самое короткое расстояние между двумя точками?

Нет, прямая линия не всегда является самым коротким расстоянием между двумя точками. Наименьшее расстояние между двумя точками зависит от геометрии объекта/поверхности. Для плоских поверхностей линия действительно является кратчайшим расстоянием, но для сферических поверхностей, таких как Земля, расстояния по большому кругу на самом деле представляют собой самое короткое расстояние.

В раннем возрасте всех нас учили, что "линия - это наикратчайшее расстояние между двумя точками". Однако, что если бы кто-то сказал вам, что эта почтенная во времени поговорка не совсем верна.

Как оказалось, это утверждение лишь отчасти правдиво. Самое короткое расстояние между двумя точками на самом деле зависит от геометрии рассматриваемого объекта.

Если бы мы жили на плоской земле (чего у нас нет), то да, прямая линия была бы наименьшим расстоянием между точками A и B. Однако, Земля - это приблизительная сфера, а наименьшее расстояние между двумя точками на поверхности сферы - это дуга, известная как "расстояние по большой окружности".

Большое расстояние круга

Большое расстояние круга не новая концепция; на самом деле, многие из вас уже видели это в действии.

Люди, которые путешествовали по воздуху или только проверяли маршруты полета, вероятно, заметили, что рейсы не следуют прямым путем, а вместо этого берут изогнутый маршрут к месту назначения. Изогнутые маршруты не используются для того, чтобы выкопать более глубокую яму в карманах пассажиров, а используются потому, что на самом деле они являются самым коротким расстоянием между любыми двумя заданными точками на нашей планете.

Эти изогнутые маршруты часто сбивают с толку, так как маршруты очерчены на плоской двухмерной карте, где прямая линия может показаться наименьшим расстоянием. Однако ни одна двумерная карта Земли не является точной.

Чтобы дать вам понять суть, наша любимая Земля является трехмерным пространством и лучше всего представлена с помощью модели глобуса. Однако, когда пытаешься сравнять сферу с прямоугольной формой, как это делают большинство карт, на первый план выходит вековая дилемма искажений. Большинство прямоугольных карт торгуют формами страны, размерами, промежуточными расстояниями и даже легитимной информацией для удобства понимания.

Представьте, что вы хотите улететь из кишащих крысами глубин Нью-Йорка в город любви, Париж. На глобусе кратчайшее расстояние между двумя городами было бы дугой примерно 3630 миль, но та же самая дуга, когда она проецируется на 2D-карту, превращается в прямую линию, измеряющую приблизительно 3750 миль.

Чтобы убедиться в этом самим, откройте Google Maps на соседней вкладке и найдите Нью-Йорк. Найдя его, щелкните правой кнопкой мыши на именном теге и выберите "измерить расстояние". Затем уменьшите масштаб или прокрутите немного вправо, чтобы найти Париж, и нажмите на него. Следующее расстояние будет представлять собой кривую, представляющую собой кратчайшее расстояние между двумя городами. Нажмите в любом месте на этой кривой, чтобы сделать ключевую фигуру, и перетащите её немного на юг, чтобы преобразовать кривую в прямую линию. Вы можете использовать несколько ключевых кадров, чтобы составить прямую линию между двумя точками. После этого сравните размеры кривой и прямой линии (и приготовьтесь к тому, что ваша реальность будет разрушена!).

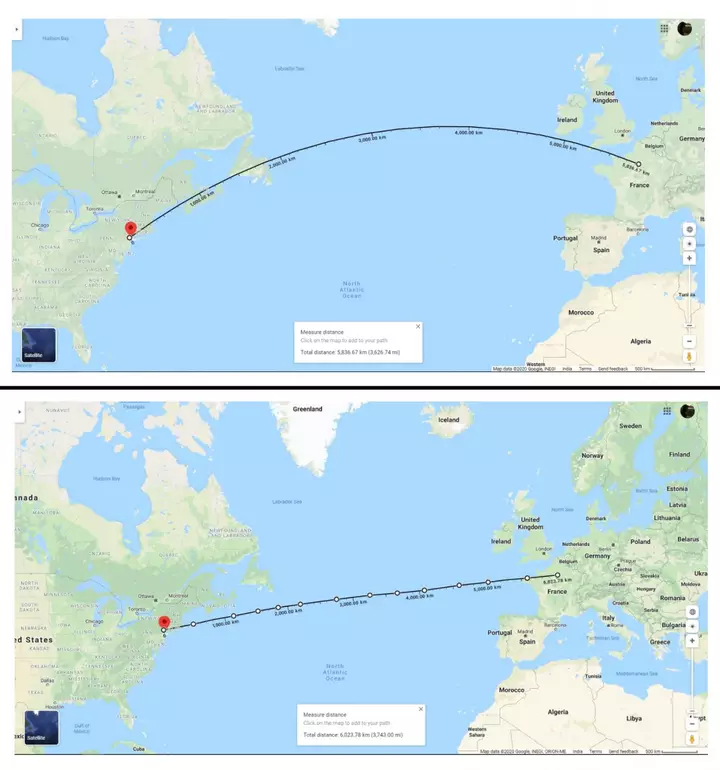
Разница между двумя числами (3,750 – 3,630 = 120 миль) может показаться несущественной, но, учитывая тот факт, что Boeing 747 потребляет в среднем 5 галлонов топлива на милю полета, самолет потребует дополнительных (5 галлонов/км × 120 миль =) 600 галлонов (2250 литров), чтобы пройти дополнительное расстояние, что является большим делом и добавит к стоимости билетов на самолет.

Расстояние большого круга в математических терминах

Говоря чисто математическим языком, большой круг (также известный как геодезические сферы) - это любой круг, нарисованный на сфере, центр которой совпадает с центром сферы, и таким образом делит сферу на две равные половины. Проще говоря, большой круг - это самый большой круг, который можно вырезать из сферы. Малый круг, с другой стороны, это когда центр круга и сферы не совпадают.

Представьте себе (или просто посмотрите на рисунок ниже), разрезая землю вдоль экватора или полюсов. Результирующие полушария в обоих случаях будут равны, и грани этих полушарий будут иметь тот же диаметр и центр, что и сама сфера (Земля).

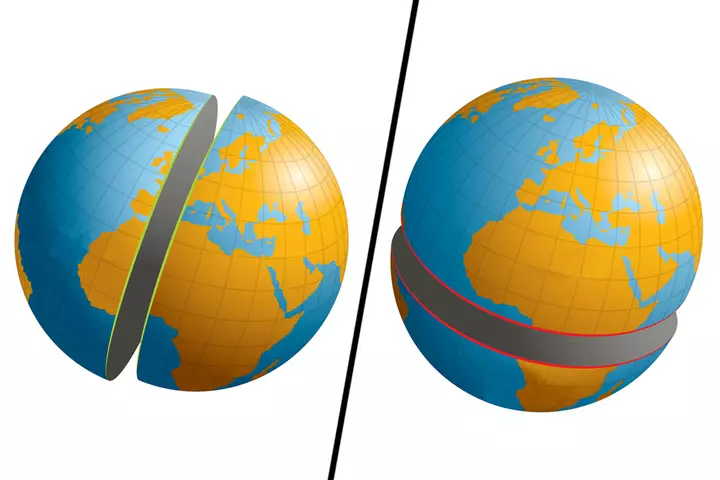
Для любых двух не диаметральных точек (положений) на сфере (Земле) существует только один уникальный большой круг, тогда как для диаметральных точек на сфере можно нарисовать бесконечное число больших кругов. Эти точки делят окружность на две дуги; меньшая дуга представляет собой истинное кратчайшее расстояние между двумя точками и называется расстоянием большого круга.

На приведенном ниже изображении точки P и Q являются двумя не диаметральными точками, а дуга PQ представляет собой кратчайшее расстояние между ними (расстояние большого круга). Точки u и v, с другой стороны, известны как противоположные или диаметрально противоположные точки и разделяют большой круг на две идентичные дуги.

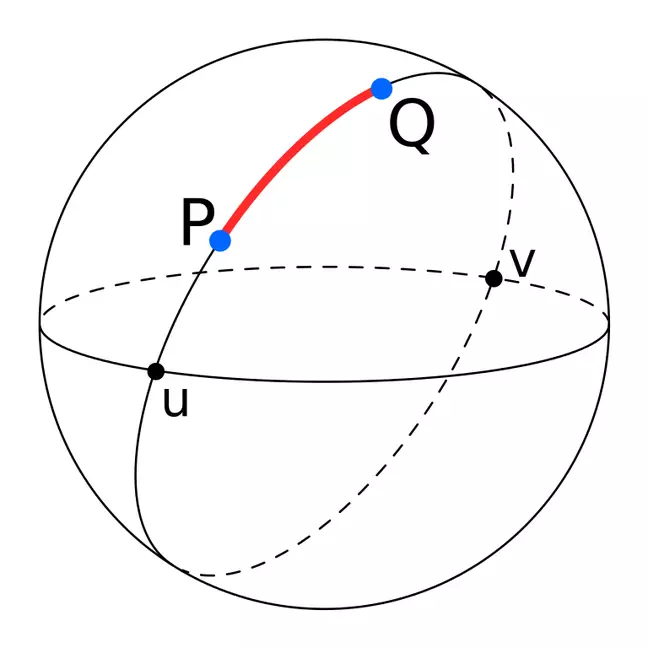
Вычисление расстояния большого круга между любыми двумя точками на поверхности сферы требует использования сферической тригонометрии, и хотя мы, возможно, не были знакомы с существованием больших расстояний круга еще в наши школьные годы, всеобщая ненависть к синусам и косинусам хорошо известна.

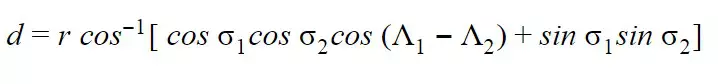
Здесь d-расстояние большого круга, r-радиус сферы (Земли) и термин cos -1 (cos σ ₁ .cos σ ₂ .cos (λ₁ – λ₂) + sin σ ₁ .sin σ ₂) - центральный угол, под которым расположены две точки с координатами σ ₁, λ ₁ и σ ₂, λ ₂ соответственно.

Как уже говорилось ранее, большие круги находят свое основное применение в дальних путешествиях, в частности в воздушной и морской навигации. Искривленный характер больших окружных расстояний, дополненный вращением нашей планеты, заставляет пилотов и моряков постоянно корректировать свой курс. Поэтому большое расстояние по окружности разбивается на "линии Румба", которые представляют собой постоянное направление.

Сказав все это, даже большие расстояния по кругу не представляют собой истинное кратчайшее расстояние между двумя заданными местоположениями. Расстояния большого круга рассчитываются исходя из предположения, что Земля является идеальной сферой, но планета представляет собой более плоскую сферу с различными значениями радиуса в направлении экватора и полюсов. Значения большого круга, таким образом, имеют допуск около ± 5%.

Тем не менее большие расстояния по окружности сыграли огромную роль в дальних поездках за последние несколько лет и будут продолжать делать это, экономя топливо авиакомпаний и экономя деньги путешественников!