Шестиугольные структуры - почему они так часто встречаются в природе

Столбы базальтов от извержения старого вулкана. Снежинка. Пчелиные ульи. Кораллы, кристаллы и множество других структур, как биологических, так и небиологических, имеют форму шестиугольника. Почему природа, которая часто кажется такой беспорядочной и неправильной, предпочитает именно эту форму? Оказывается, все дело в геометрии и физике.

Пчелы тратят много времени на работу, но они не любят работать впустую - пчелы ничто, если они не эффективны. Пчелы также эффективно строят свои соты, и шестигранная форма помогает в этом.

Соты строятся из пчелиного воска, вырабатываемого рабочими пчелами. Они вырабатывают воск из специальных желез в своем теле, которые затем смешивают с небольшим количеством меда и пыльцы, которую они разжевывают, чтобы получить пчелиный воск. Соты будут служить сосудами для хранения меда, а также камерами для выращивания молодых пчел.

Все это хорошо и замечательно, но почему шестиугольники?

Древние философы тоже задавались этим вопросом. Греческий философ Папп Александрийский, изучавший шестиугольники более 1 600 лет назад, считал, что пчелы обладают "определенным геометрическим мышлением", а энтомолог Уильям Кирби полагал, что пчелы - это "математики, наученные небесами". Даже Чарльз Дарвин интересовался шестиугольниками пчел и проводил эксперименты, чтобы выяснить, могут ли пчелы строить шестиугольные соты, используя только свои инстинкты, или это обучаемое поведение.

Ко времени Дарвина люди довольно хорошо понимали геометрию шестиугольников - особенно когда речь шла о покрытии поверхностей. Если вы хотите использовать одну форму и только одну форму для покрытия плоской поверхности, есть только три формы, которые работают: равносторонние треугольники, квадраты и шестиугольники. Из них шестиугольники используют наименьшее количество разделительной стенки, поэтому логично, что пчелы предпочитают именно их, поскольку это означает, что им нужно использовать меньше пчелиного воска. Как заявил Дарвин, это самое эффективное решение, и шестиугольные соты "абсолютно идеальны в экономии труда и воска". Пчелы действительно были наделены некоторыми геометрическими способностями.

Пчелы - далеко не единственные существа, использующие шестиугольники. Кожица в центральной части панциря черепах имеет шестиугольную форму - опять же, потому что это такой эффективный способ покрытия поверхности. Но шестиугольники не очень хорошо работают на изогнутых поверхностях, таких как панцирь черепахи, поэтому в панцире также есть кольцо пятиугольников и неправильных форм.

Вымерший коралл Cyathophyllum hexagonum даже назван в честь своей шестиугольной формы, а некоторые диатомовые водоросли (основная группа водорослей) также имеют шестиугольную форму. Но, пожалуй, ни одна биологическая структура не имеет такой поразительной шестиугольной формы, как глаза стрекоз.

Глаза, состоящие примерно из 30 000 шестиугольников, переплетенных в ослепительное множество, являются одними из лучших в животном мире. Фактически, глаза стрекоз состоят из правильных шестиугольников, причем только три из этих шестиугольников встречаются в любой данной точке пересечения (или вершине).

У стрекоз два больших сложных глаза с тысячами шестиугольных линз (а также три глаза с простыми линзами, но оставим их пока в стороне). Шестиугольные линзы соединены между собой длинным тонким сетчатым каналом. На самом деле, у многих насекомых глаза имеют шестиугольную форму, и правило всегда гласит, что только три стенки клетки могут встречаться в любой вершине.

На самом деле, если мы на мгновение отойдем от биологического мира, то обнаружим, что точно такое же правило управляет чем-то совершенно другим: пеной из пузырьков.

Хотя пена пузырьков остается трудноразрешимой математической задачей, известно, что пена часто имеет тенденцию образовывать шестиугольные формы. В данном случае речь идет о поиске структуры с наименьшим общим поверхностным натяжением (что означает наименьшую площадь стены из мыльной пленки), и эта форма оказывается шестиугольником.

Конечно, структуры пены редко бывают идеально шестиугольными (а иногда они вообще не шестиугольные), потому что они также должны быть механически устойчивыми (и противостоять таким вещам, как ветер). Что еще более усложняет ситуацию, трехмерное расположение делает проблему еще более сложной. Несмотря на склонность к шестиугольникам, пена редко бывает упорядоченной.

На самом деле было удивительно много споров о том, какие формы может принимать пена, исследователи предлагали трехмерные 14-гранные многогранники и даже некоторые более безумные и беспорядочные формы. Но именно здесь становится интересно. Правила, управляющие формой ячеек в пене, похоже, также управляют некоторыми формами живых клеток. Дело не только в том, что глаза некоторых мух имеют такие же шестиугольные узоры, как и пена пузырьков, но и в том, что клетки внутри отдельных линз сгруппированы таким образом, что, похоже, повторяют геометрию пены пузырьков. Это поразительный случай, когда физика и математика направляют формы в биологическом мире.

Пена - далеко не единственная шестиугольная форма в природе. Возможно, наиболее ярким примером является вулканическое столбчатое соединение.

Некоторые вулканические извержения (особенно те, которые порождают базальтовые породы) могут порождать поразительные шестиугольные образования, которые озадачивали людей на протяжении веков. Подобные образования есть во многих местах по всему миру - от как бы шестиугольных до почти идеально шестиугольных. К счастью, у нас есть довольно хорошее представление о том, как они образуются.

Когда вулкан извергается, он может извергать горячую лаву. Вытекая на поверхность, лава начинает остывать - и по мере остывания она сжимается. Это сжатие создает все большее и большее давление, и в конце концов образуются трещины. Как выяснилось, угол, который создает наибольшее напряжение, составляет 120 градусов - это, если вы помните, внутренний угол в правильном шестиугольнике.

Но не вся лава остывает в одно и то же время, и некоторые участки могут все еще течь, в то время как другие уже затвердели, что может сделать формы более несовершенными. Поразительно, что часто угол удивительно близок к 120 градусам.

Если вы все еще не верите в существование шестиугольников в природе, вот еще один пример: снежинки.

Конечно, каждая снежинка уникальна, но все снежинки имеют шесть сторон или точек, и это связано с тем, как они формируются. Внешняя форма снежинок отражает их внутреннюю структуру. Гексагональная структура позволяет молекулам воды (с одним атомом кислорода и двумя атомами водорода) группироваться вместе наиболее эффективным образом.

На самом деле, если увеличить масштаб, снежинки - далеко не единственные кристаллы, имеющие шестиугольную структуру. Существует целое семейство кристаллов (так называемое семейство гексагональных кристаллов), внутренняя структура которых состоит из шестиугольников или структур гексагонального типа.

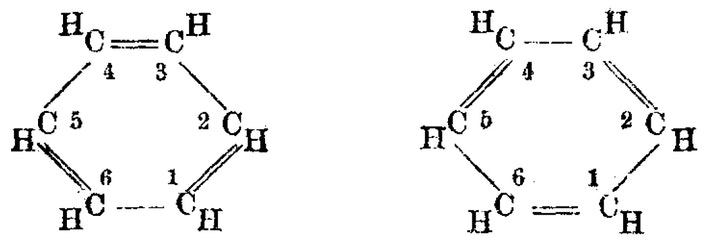
Если мы еще больше увеличим масштаб, то обнаружим еще одну форму шестиугольника. Как быстро отметит любой студент-химик, шестиугольники являются основой органической химии. Когда шесть атомов углерода соединяются, угол составляет 120 градусов, что уже должно быть знакомо. Шесть соединенных атомов углерода образуют идеальный шестиугольник, который также называется бензольным кольцом.

Есть еще один пример, который мы должны рассмотреть, и мы перейдем от очень маленьких к очень большим. Планета Сатурн имеет один из самых необычных шестиугольников в Солнечной системе: облачный узор длиной около 14 500 км; он больше, чем весь диаметр Земли. Шестиугольник состоит из газов, движущихся со скоростью 320 км/ч, и, как полагают, имеет толщину до 300 км.

Исследователи точно не знают, почему так происходит, но уже выдвинуто несколько теорий.

Почему же шестиугольники так часто встречаются в природе? Это зависит от того, как на это посмотреть. Это может быть эффективный способ сохранения массы или энергии, или просто способ расположить атомы таким образом, чтобы они были стабильны. Это может быть просто что-то, обусловленное геометрией.

Природе, как правило, не нравятся очень фиксированные вещи - но она любит узоры, и иногда ей нравятся шестиугольники. Возможно, зная и осознавая это, мы сможем получать еще больше удовольствия от этих шестиугольников, когда столкнемся с ними.