Самый простой способ решения квадратичных уравнений упускается из виду в течение 4000 лет
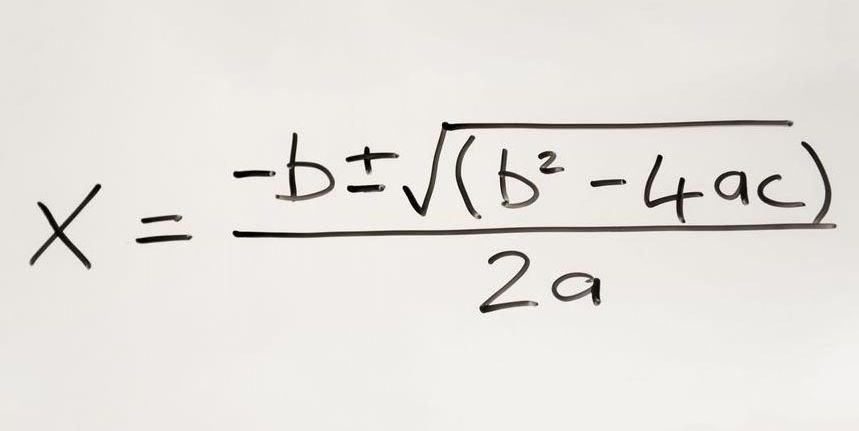
Профессор математики открыл новый способ решения квадратных уравнений. Это вычислительно эффективнее и проще для запоминания, чем традиционная квадратичная формула. Удивительно, что такой простой метод оставался незамеченным в течение 4000 лет.
В элементарной алгебре квадратные уравнения могут быть решены с использованием различных методов, таких как факторинг, построение графиков, построение квадратов и другие.
История квадратичной формулы - формула обеспечивает решение (я) квадратного уравнения - может быть прослежена до древне-вавилонского периода около 2000–1600 гг. До н.э. Многие великие математики оставили свой след на этом предмете, и формула стала одной из самых важных частей в алгебре.
Формула, однако, довольно сложна, и ее вычисления несколько запутаны. Это может быть сложной задачей для начинающих изучающих алгебру.
Недавно математик из Университета Карнеги-Меллона в Питтсбурге опубликовал более простое решение для любого квадратного уравнения. Этот новый метод прост в запоминании и эффективен в вычислительном отношении.
По словам его автора, , он имеет потенциал для демистификации квадратичной формулы для студентов во всем мире.
Альтернативный метод решения квадратичных задач
Самый первый шаг - посмотреть, можно ли разложить квадратное уравнение следующим образом:

Если факторизация возможна, то квадратичная функция равна нулю при X=R или X=S. Согласно традиционному методу, если сумма и произведение R и S равно -B и C соответственно, то {R, S} будет полным набором корней.
А вот теперь начинается поворот.
Два числа суммируют с -B именно тогда, когда их среднее значение равно -B / 2. Рассмотрим эти два числа в виде -B / 2 ± z, где z - неизвестная величина, а произведение этих чисел равно C.
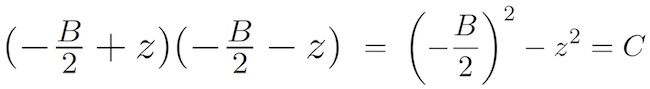
Если z оказывается равным нулю, то мы разложим с R = S = (- B / 2), в противном случае,
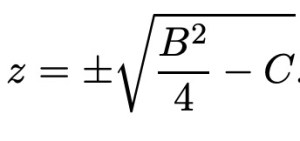
Квадратный корень всегда существует (с учетом комплексных чисел), поэтому искомые R и S всегда существуют для любого квадратичного уравнения. Таким образом, исходные корни могут быть выражены как

А, это новая квадратичная формула; гораздо проще и легче запомнить, чем предыдущий.
Почему сейчас?
Новый метод интуитивно понятен и не требует запоминания формулы вообще. Однако, более интересный вопрос, почему никто не думал об этом раньше.
Автор исследовал 4000-летнюю историю по этой теме: он изучал различные подходы, построенные древними вавилонянами, греками, индийцами, арабами и китайцами, а также современными математиками, но не нашел ничего похожего на его метод.
По-Шен Ло считает, что это связано с тем, как традиционный метод доказывает, что квадратные уравнения имеют два корня. Обычно считается, что квадратное уравнение всегда имеет два корня, и эти корни имеют произведение C и -B.
Возможно, к тому времени, когда математика продвинулась до "приличного уровня", Вавилонская техника исчезла из недавней памяти, и люди нашли подход завершения квадрата достаточно хорошим, чтобы интегрироваться в основную учебную программу.
Теперь вопрос в том, как быстро и насколько широко он будет распространяться.
Ссылка: :1910.06709