Прыжок в континуум
Точное вычисление динамики многих взаимодействующих квантовых частиц является сложной задачей. Однако для таких систем существует многообещающий метод расчета: тензорные сети, которые исследуются в отделе теории Института квантовой оптики им. Макса Планка. Первоначальный фокус тензорной сети был сосредоточен на квантовых частицах, ограниченных решеткой, как, например, они встречаются в кристаллах или в квантовых регистрах будущих квантовых компьютеров. В новой статье постдокторскому исследователю Антуану Тиллой и директору отдела теории Игнасио Чираку удалось распространить этот подход на континуум. Целью в долгосрочной перспективе является элегантный метод расчета квантовых теорий поля, который описывает основные силы физики.
Описание систем, в которых многие квантовые частицы взаимодействуют и коллективно порождают новые явления, является одной из фундаментальных задач физики. Одним из примеров такого квантового явления многих тел является сверхпроводимость. Трудность в том, что частицы влияют друг на друга. В результате квантово-механические уравнения, которые описывают это коллективное поведение, могут быть получены, но не решены точно.
В квантовой механике динамическое уравнение должно охватывать все возможные состояния, в которых потенциально может находиться система. И их может быть много. Примером, в настоящее время популярным в физике, являются квантовые биты. Они получены, например, из специально подготовленных электронов или электрически заряженных атомов. Такие кубиты имеют два противоположных состояния, которые могут принимать значения ноль и одно. Но в отличие от «классического» бита, кубит также может находиться в любой суперпозиции этих двух состояний. Если теперь один соединяет два кубита с так называемыми квантовыми воротами, абстрактное математическое пространство всех возможных квантовых состояний удваивается. И каждый дополнительный кубит снова удваивает его. Процессоры и память данных обычных компьютеров буквально переполнены этим экспоненциально растущим числом возможных квантовых состояний. Даже суперкомпьютеры выходят из строя после нескольких десятков кубитов. Только квантовые компьютеры, подчиняющиеся правилам самой квантовой механики, однажды смогут справиться с динамикой больших квантовых систем.
Делая неисчислимое исчисляемым
Пример кубитов подходит, потому что Игнасио Чирак и его коллеги являются одними из пионеров этой новой области квантовых информационных технологий. Метод «тензорных сетей», который является предметом данной статьи, также происходит из этой области исследований. Это позволяет хитро уменьшить гигантское пространство всех возможных квантовых состояний многочастичной системы до вычисляемого размера. «Представьте себе все возможные квантовые состояния многочастичной системы как огромную круглую область», - объясняет Антуан Тиллой. «Но состояния, которые действительно актуальны для нашей системы, укладываются в гораздо меньший круг». Искусство сейчас заключается в том, чтобы найти этот маленький круг в абстрактном математическом пространстве, и это то, что могут сделать тензорные сети.
Тиллой - постдокторский исследователь в группе Чирака, и вместе они только что опубликовали статью о тензорных сетях в журнале Physical Review X. Первоначально физики применяли их к массивам отдельных кубитов. Таким образом, тензорные сети изначально полагались на сетку абстрактных математических объектов - немного похоже на математическую цепочку жемчужин, живущих в дискретных позициях.
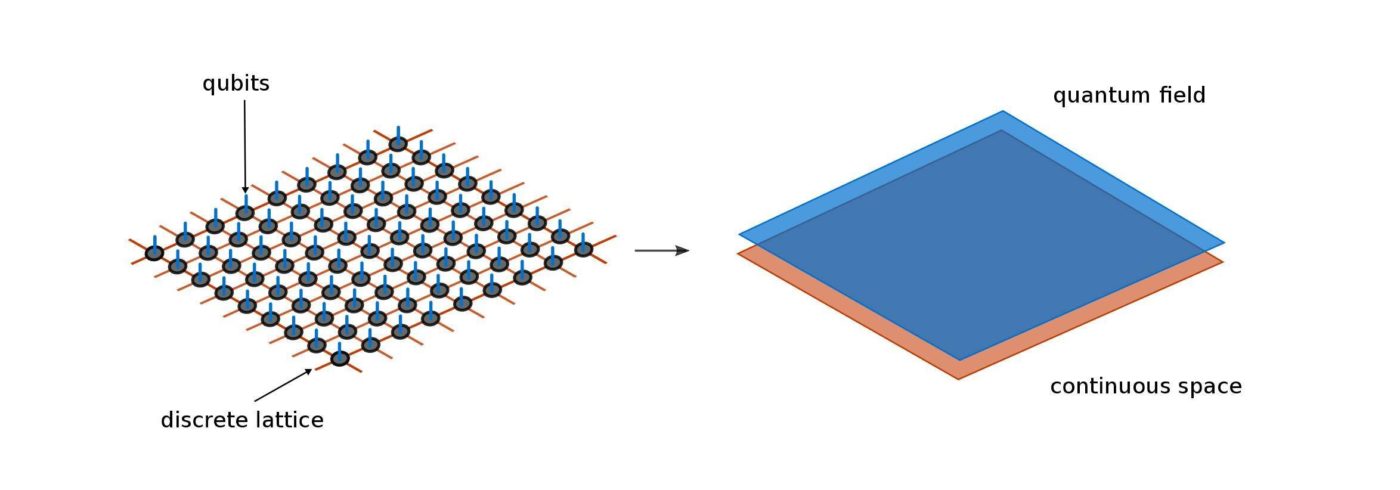
Тензорные сети оказались успешным инструментом для проведения вычислений для большого класса квантовых систем, ограниченных сетками. Этот успех дал теоретическим исследовательским группам по всему миру идею: может ли этот метод также применяться к физическим системам, которые живут не на сетках, а в континуальном пространстве? Короче говоря, ответ - да. Фактически, метод тензорных сетей может быть расширен до континуума, и это то, что Тиллой и Чирак продемонстрировали в своей новой работе.
Новый инструмент для квантовых теорий поля
Так называемые квантовые теории поля могут быть важной областью применения этого нового набора инструментов. Эти теории составляют основу современного физического мировоззрения. Они точно описывают, как три из четырех основных сил физики функционируют в соответствии с квантовой механикой. Эти силы опосредованы виртуальными частицами, которые существуют только в течение короткого периода времени, необходимого для передачи их силы.
Например, в электрической силе опосредующие частицы представляют собой виртуальные световые кванты. «Это подпадает под так называемую квантовую электродинамику и хорошо понято», - говорит Тиллой. «Ситуация усложняется тем, что известно как квантовая хромодинамика». КХД, как ее кратко называют, описывает силы между кварками, которые в свою очередь образуют строительные блоки атомных ядер, протонов и нейтронов. Глюоны, «адгезивные частицы», опосредуют самую сильную силу в физике. И это «склеивает» кварки вместе.
Но в отличие от виртуальных фотонов, глюоны также могут сильно влиять друг на друга. Это «самодействие» приводит к неприятному факту, что уравнения КХД могут быть решены только в пограничных случаях при очень высокой энергии. Для более низких энергий - нормальное состояние материи в нашей среде - это невозможно. По этой причине физикам пока приходится работать с приближенными решениями. Стандартным шагом здесь является разбиение континуума на искусственную сетку точек, для которой мощный компьютер может затем вычислить приближенные решения.
«Этот этап дискретизации является сложным, - говорит Тиллой. Кроме того, такие упрощения всегда имеют недостаток, заключающийся в нарушении фундаментальной симметрии природы при делении континуума на сетку дискретных точек. Таким образом, они вынуждены отойти от реальной физики. Здесь может помочь метод непрерывных тензорных сетей, потому что он не требует этой предварительной дискретизации пространства. Возможно, поведение кварков и глюонов при низких энергиях когда-нибудь станет понятным. Сегодня это все еще открытая проблема, но недавно обнаруженные непрерывные тензорные сети уже могут быть частью решения.