Новый эксперимент показывает, что принцип неопределенности не так неопределенен, как мы думали

Слово неопределенность часто используется в квантовой механике. Одна мысль состоит в том, что это означает, что в мире есть что-то, в чем мы не уверены. Но большинство физиков считают, что сама природа неопределенна.
Внутренняя неопределенность была центральной в том, как немецкий физик Вернер Гейзенберг, один из создателей современной квантовой механики, представил теорию.
Он выдвинул принцип неопределенности, который показал, что мы никогда не можем знать все свойства частицы одновременно.
Например, измерение положения частицы позволит нам узнать ее положение. Но это измерение обязательно нарушит его скорость на величину, обратно пропорциональную точности измерения положения.
Был ли Гейзенберг неправ?
Гейзенберг использовал Принцип неопределенности, чтобы объяснить, как измерение может разрушить эту классическую особенность квантовой механики, двухщелевую интерференционную картину (подробнее об этом ниже).
Но еще в 1990-х годах некоторые выдающиеся квантовые физики утверждали, что доказали, что можно определить, через какую из двух щелей проходит частица, без существенного нарушения ее скорости.
Значит ли это, что объяснение Гейзенберга должно быть неверным? В работе, только что опубликованной в Science Advances, мои экспериментальные коллеги и я показали, что было бы неразумно делать такой вывод.
Мы показываем, что нарушение скорости - размера, ожидаемого от принципа неопределенности, - всегда существует в определенном смысле.
Но прежде чем углубляться в детали, нам нужно кратко объяснить двухщелевой эксперимент.
Двухщелевой эксперимент
В этом типе эксперимента есть барьер с двумя отверстиями или щелями. У нас также есть квантовая частица с неопределенностью положения, достаточно большой, чтобы покрыть обе щели, если она выстрелит в барьер.
Поскольку мы не можем знать, через какую щель проходит частица, она действует так, как если бы она проходила через обе щели.
Признаком этого является так называемая «интерференционная картина»: рябь в распределении того места, где частица может быть обнаружена на экране в дальнем поле за щелями, что означает длинный путь (часто несколько метров) за щелями.
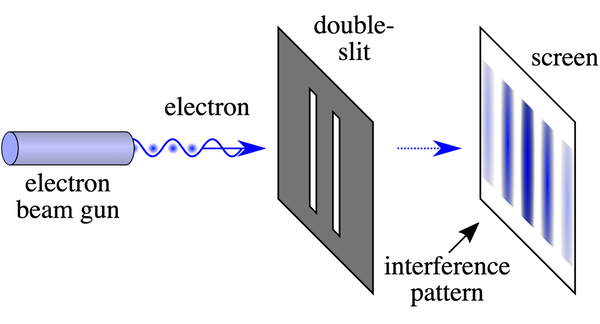
Но что, если мы поместим измерительное устройство рядом с барьером, чтобы выяснить, через какую щель проходит частица? Увидим ли мы еще интерференционную картину?
Мы знаем, что ответ отрицательный, и объяснение Гейзенберга состояло в том, что если измерение положения будет достаточно точным, чтобы определить, через какую щель проходит частица, это даст случайное возмущение ее скорости, достаточно большое, чтобы повлиять на то, где она окажется в дальнем поле. и, таким образом, смыть рябь помех.
Выдающиеся квантовые физики поняли, что обнаружение, через какую щель проходит частица, не требует измерения положения как такового. Подойдет любое измерение, которое дает разные результаты в зависимости от того, через какую щель проходит частица.
И они придумали устройство, которое воздействует на частицу не так, как случайный скачок скорости. Следовательно, они утверждали, что не принцип неопределенности Гейзенберга объясняет потерю помех, а какой-то другой механизм.
Как и предсказывал Гейзенберг
Нам не нужно вдаваться в то, что, как они утверждали, было механизмом уничтожения помех, потому что наш эксперимент показал, что влияние на скорость частицы оказывает только предсказанный Гейзенбергом размер.
Мы увидели то, что упустили другие, потому что это нарушение скорости не происходит, когда частица проходит через измерительное устройство. Скорее это задерживается до тех пор, пока частица не пройдет мимо щелей на пути к дальнему полю.
Как это возможно? Ну, потому что квантовые частицы на самом деле не просто частицы. Они тоже волны.
Фактически, теория, лежащая в основе нашего эксперимента, была той, в которой проявляется природа волны и частицы - волна направляет движение частицы в соответствии с интерпретацией, предложенной физиком-теоретиком Дэвидом Бомом, поколением после Гейзенберга.
Давай поэкспериментируем
В нашем последнем эксперименте ученые в Китае следовали методике, предложенной мной в 2007 году, для восстановления гипотетического движения квантовых частиц из множества возможных начальных точек через обе щели и для обоих результатов измерения.
Они сравнивали скорости с течением времени, когда не было измерительного устройства, с теми, когда они были, и таким образом определяли изменение скоростей в результате измерения.
Эксперимент показал, что влияние измерения на скорость частиц продолжалось еще долго после того, как частицы очистили само измерительное устройство, на расстоянии 5 метров от него.
К этому моменту в дальнем поле кумулятивное изменение скорости было в среднем достаточно большим, чтобы вымыть рябь в интерференционной картине.
Итак, в конце концов принцип неопределенности Гейзенберга торжествует.
Взять домой сообщение? Не делайте далеко идущих утверждений о том, что принцип может или не может объяснить явление, пока вы не рассмотрели все теоретические формулировки принципа.
Да, это немного абстрактное сообщение, но это совет, который может применяться в областях, далеких от физики.
, директор Центра квантовой динамики .
Эта статья переиздана из беседы под лицензией Creative Commons. Прочитайте .