Математики открыли «тайную геометрию» жизни

Математики выявили новую категорию геометрических фигур, которые в изобилии встречаются в природе. Эти формы, в отличие от обычных фигур, более точно соответствуют сложной структуре природных элементов.
Геометрические фигуры могут быть определены с помощью точных уравнений и отличаются четкими контурами и точками. Благодаря этим характеристикам их легко анализировать с геометрической точки зрения. Однако известные на сегодняшний день геометрические формы не всегда соответствуют тем, что встречаются в природе. На самом деле природные элементы, как правило, имеют более сложные контуры, изогнутые поверхности и нерегулярные структуры, которые нелегко описать простыми уравнениями.
Это недавно побудило математиков из Будапештского технологического университета исследовать новые геометрические формы и разработать математические теории, которые могли бы лучше отразить разнообразие и сложность природных форм.
Они выделили новый класс форм, которые назвали "мягкими клетками". Эти формы характеризуются изогнутыми краями и отсутствием жестких углов, что явно отличает их от обычных геометрических фигур. Благодаря этому открытию работа венгерских исследователей должна способствовать улучшению нашего понимания участия математики в моделировании природных явлений. Подробности доступны на сервере предварительной публикации .
Эти новые фигуры — мягкие клетки — описываются как своего рода плитка с изогнутыми краями. И несмотря на такую нетрадиционную форму, они могут быть расположены таким образом, чтобы образовывать целостные структуры как в двух, так и в трех измерениях. По словам исследователей, они действительно могут "плавно" деформироваться, образуя мягкую плитку.
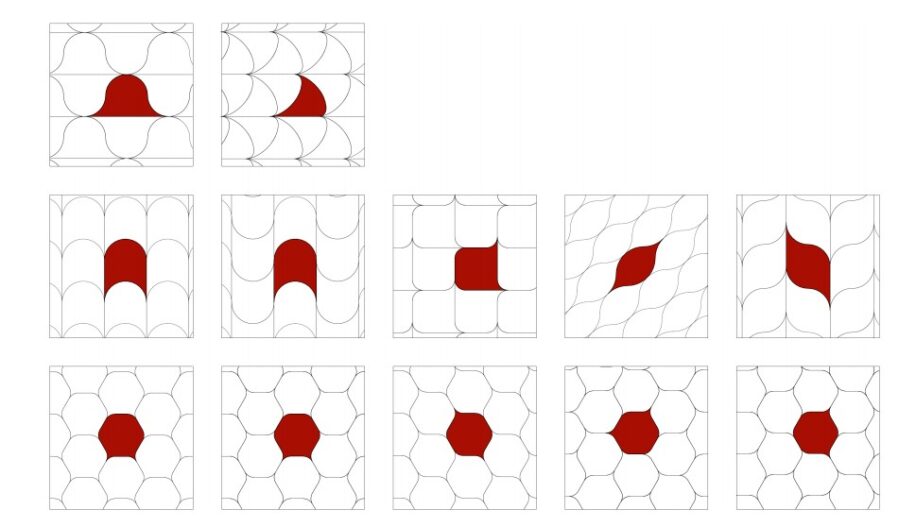
Очень интересным аспектом этих новых фигур является их применение к "тесселированию пространства" в природных элементах, что до сих пор было одной из основных проблем геометрии, по словам исследователей, участвовавших в работе. В информационных целях под укладкой понимается покрытие поверхности или объема повторяющимися фигурами, без перекрытий или пустого пространства. В природных элементах укладка не всегда соответствует строгим геометрическим правилам. Это связано с нерегулярностью их поверхностей и относительным отсутствием острых углов в их структуре.
Формы, распространенные в природе
Исследователи также обнаружили, что эти недавно описанные формы широко распространены в природе. В частности, они приводят многочисленные природные объекты, такие как биологические клетки, раковины и, возможно, даже некоторые виды органических тканей, которые демонстрируют геометрические характеристики, далекие от жестких форм, изучаемых в математике.
Что касается последствий этого открытия, то соответствие этих форм для создания плиток различных двумерных и трехмерных структур может найти применение в различных областях, таких как биология (где они могут предложить модели, адаптированные к структуре живой ткани) или инженерия, где эти геометрические формы могут вдохновить на создание более эффективных и прочных структур.