Какова цель поиска корреляции? Почему это используется, если корреляция не подразумевает причинно-следственную связь?
Приходилось ли вам сталкиваться со странными статистическими данными о двух событиях, которые на первый взгляд не связаны между собой? Например, если попросить человека предсказать продажи кондиционеров, основываясь только на данных о продажах мороженого, предсказание может показаться нелепым. В конце концов, кондиционеры и мороженое - это два разных потребительских товара, производимых несвязанными отраслями. Можно утверждать, что мороженое имеет столько же общего с кондиционером, сколько планета Земля с кометой Хейла.
Или вот, например: В первой половине 2020 года средства массовой информации были переполнены информацией об этом исследовании, в котором температура коррелировала с передачей COVID-19. Однако это исследование, проведенное на основе данных за тот же промежуток времени, в котором был сделан обратный вывод, не получило такого же внимания. Почему это так? Значит ли это, что поиск корреляции бесполезен?
Или вот, например: В первой половине 2020 года средства массовой информации были переполнены информацией об этом исследовании, связанном с корреляцией температуры с передачей COVID-19. Тем не менее это исследование, проведенное на данных, доступных за тот же временной интервал, в котором был сделан иной вывод, не привлекло подобного внимания. Почему это так? Означает ли это, что обнаружение корреляции бесполезно? Нет.
Давайте сначала разберемся, что такое корреляция, прежде чем приступать к поиску ее достоинств. Затем мы перейдем к причинно-следственной связи.
Поиск смысла в случайных данных: Исследовательский анализ
Событие - это любое явление, которое поддается наблюдению (может быть записано в виде числа). Например, продажа кондиционеров, оценки, полученные учениками в классе, голы, забитые игроком, и т.д. Эти случайные события из реальной жизни хранятся в виде данных, на основании которых продавцы, учителя и тренеры могут делать определенные выводы.
Когда для случайного события доступно много точек данных (числовых значений), событие называется случайной переменной (случайной, потому что значения, которые они принимают, нельзя предсказать до наступления события, и переменной, потому что значения меняются при каждом новом появлении).
При рассмотрении двух случайных величин может оказаться, что между ними существует некоторая связь, которая поможет лучше понять события и сделать точные прогнозы относительно будущего исхода указанных событий. Это очень удобно при наличии ограниченного количества исходных данных.
Необходимо ввести два основных статистических понятия, которые помогут нам лучше понять корреляцию.
Первое - это дисперсия. Если случайная переменная X имеет n точек данных, дисперсия описывает среднее отличие каждой точки данных от среднего значения X. При построении графика дисперсия показывает разброс значений. Более разбросанный набор данных будет иметь более высокую дисперсию, чем близко расположенный набор данных.
Вторая - ковариация. Учитывая две случайные переменные X и Y, изменение значений одной переменной может быть связано или не связано с изменением значений другой переменной. Ковариация присваивает числовое значение этой тенденции изменения значений.
Корреляция
Корреляция - это математический инструмент, используемый для выявления связи между двумя случайными событиями. Цель состоит в том, чтобы выяснить степень близости разрозненных точек к прямой линии (линейная связь). Учитывая n точек данных о двух событиях X и Y, корреляция, r, определяется следующим образом:
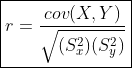
где,
cov(X, Y) = ковариация между X и Y
Что является целью поиска корреляции? Почему она используется, если корреляция не подразумевает причинно-следственную связь?,
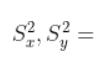
Из математического определения корреляции, всегда 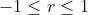
Возникают следующие случаи:
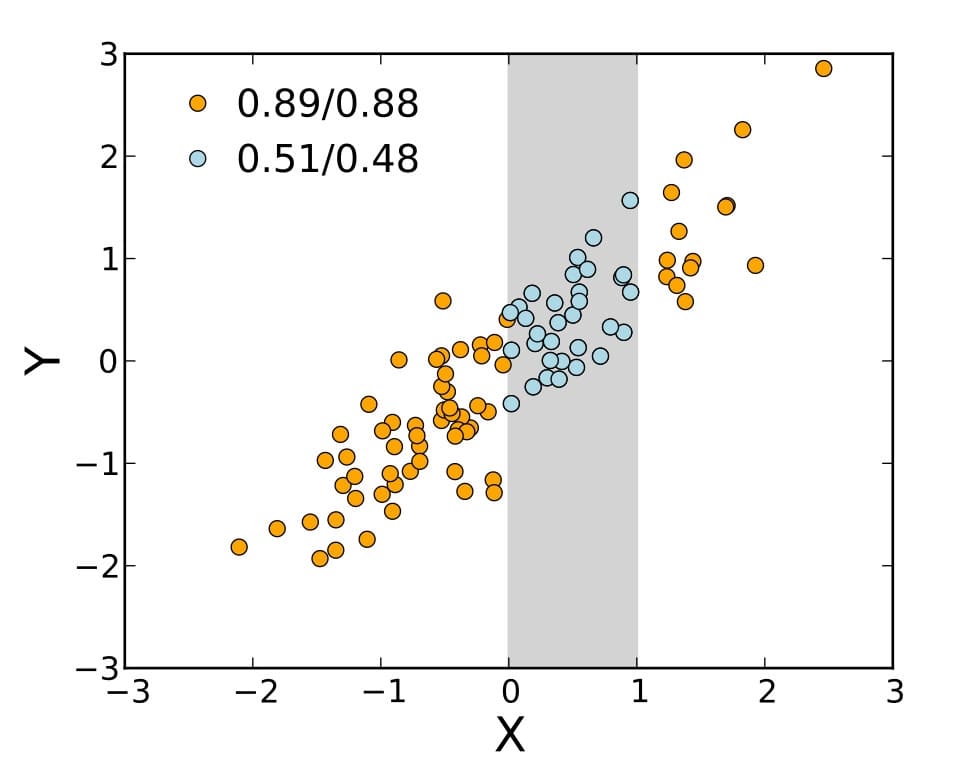
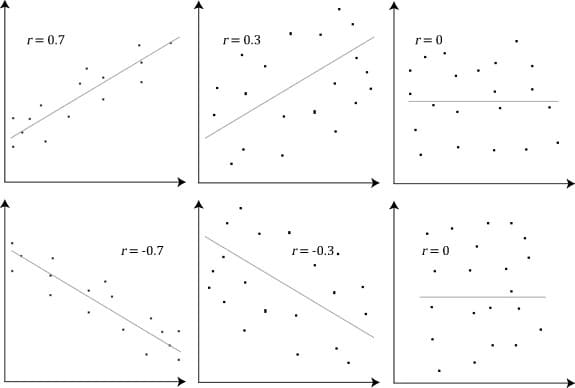
Если r=1, то точки данных лежат на прямой линии и рассеяния нет. Мы говорим, что X линейно коррелирует с Y. Это означает, что изменение X приводит к пропорциональному изменению Y, которое на графике представляет собой прямую линию с положительным наклоном.
Если r=-1, то точки данных также лежат на прямой линии и рассеяния нет. X по-прежнему линейно коррелирует с Y. Но изменение X приводит к обратно пропорциональному изменению Y, которое на графике представляет собой прямую линию с отрицательным наклоном.
Если -1 < r < 0, то точки остаются рассеянными вокруг наилучшей аппроксимирующей линии с отрицательным наклоном.
Если 0 < r < 1, то точки остаются разбросанными вокруг аппроксимирующей прямой с положительным наклоном.
Корреляция не может подразумевать причинно-следственную связь
Изучив основы корреляции, давайте углубимся в ее интерпретацию. Часто, весьма ошибочно, корреляция между двумя случайными величинами X и Y интерпретируется как причинно-следственная связь, т.е. X вызывает Y. Возьмем пример с продажами кондиционеров (X) и проданным мороженным (Y). Если обнаружена положительная корреляция (скажем, r = 0,8), означает ли это, что X вызвал Y или наоборот? Нет. Это означает, что, вероятно, существует какой-то другой фактор (Z), который является общим для X и Y. Что может быть Z?
Какая случайная переменная может вызвать положительное изменение продаж кондиционеров и мороженого? Этой случайной переменной, вероятно, может быть температура.
Подумайте об этом. Мороженое - это десерт, вероятность потребления которого летом гораздо выше, чем в другие сезоны. Повышение температуры вполне может привести к тому, что больше людей будут покупать такие десерты, чтобы охладиться. Аналогичным образом, кондиционеры регулируют температуру в помещении, что очень полезно в летний сезон. Повышение температуры может заставить даже самых закаленных людей купить кондиционер. Таким образом, повышение температуры может привести к росту продаж кондиционеров, или, проще говоря, Z вызывает X и Y.
Здесь связь между (Z, X) и (Z, Y) является причинно-следственной. Мы можем предсказать, что увеличение X будет связано с увеличением Y. Мы можем сделать такое предсказание благодаря знанию общей переменной Z (температура). Корреляция помогла нам найти причинный фактор, стоящий за этими двумя событиями.