Как доказать что Земля круглая

В последнее время, когда теоретики плоской Земли стали более громкими, кажется, что люди все чаще задают вопросы именно этого характера, и это движение набирает силу. Эти вопросы идут вразрез со всеми логическими объяснениями того, что мы знаем о нашей планете: в основном, что она имеет форму шара и вращается вокруг Солнца.
Рост популярности теорий о плоской Земле может быть результатом того, что в нашем обществе быстро становится известным как «эра постфактов/постправды», когда ложь, повторяемая достаточно много раз, становится истиной группового мышления.
К счастью, на каждую идею о том, почему Земля может быть плоской, есть вещественные доказательства, которые доказывают, что Земля определенно является шаровидной. Вот несколько доказательств, и вам даже не нужно тратить 1 миллион долларов, чтобы запустить себя в космос.
1. Луна
Теперь, когда человечество вполне позитивно знает, что Луна - это не кусок сыра и не лунный бог, явления, которые ей сопутствуют (от месячных циклов до лунных затмений), хорошо объяснены. Однако для древних греков это было большой загадкой, и в своем стремлении к знаниям они пришли к нескольким проницательным наблюдениям, которые помогли человечеству определить форму нашей планеты.
Аристотель (который сделал довольно много наблюдений о сферической природе Земли) заметил, что во время лунных затмений (когда орбита Земли размещает ее непосредственно между Солнцем и Луной, создавая при этом тень) тень на поверхности Луны имеет круглую форму. Эта тень принадлежит планете, и это отличная подсказка о сферической форме Земли.

Поскольку земля вращается (см. эксперимент "", если вы сомневаетесь), последовательная овальная тень, которую она производит при каждом лунном затмении, доказывает, что земля не только круглая, но и сферическая - абсолютно, вне всякого сомнения, а не плоская.
2. Корабли и горизонт
Если в последнее время вы были рядом с портом или просто гуляли по пляжу и смотрели вдаль на горизонт, вы могли заметить очень интересный феномен: Приближающиеся корабли не просто "появляются" за горизонтом (как это должно было бы случиться, если бы мир был плоским), а, наоборот, кажутся выходящими из-под моря.
Но, как вы говорите, корабли не могут погружаться под воду и не поднимаются из-под воды по мере приближения к нам (за исключением Пиратов Карибского моря, но мы предполагаем, что это был вымышленный сериал фильмов). Причина, по которой корабли выглядят так, как будто они "выходят из волн", заключается в том, что мир не плоский: он круглый.
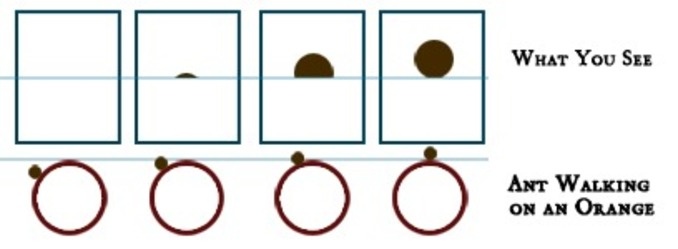
Представьте себе муравья, идущего по поверхности апельсина в поле вашего зрения. Если вы посмотрите на апельсин, вы увидите тело муравья, медленно поднимающееся из-за "горизонта" из-за кривизны апельсина. Если вы проделаете этот эксперимент с муравьем, приближающимся по длинной дороге, а не по круглому объекту, эффект изменится: муравей будет медленно «материализоваться» в поле зрения (в зависимости от того, насколько остро ваше зрение).
3. Различные звездные созвездия
Изначально это наблюдение было сделано Аристотелем (384-322 гг. до н.э.), который объявил Землю круглой, судя по разным созвездиям, которые можно увидеть, удаляясь от экватора.
Вернувшись из поездки в Египет, Аристотель отметил: "В Египте и... на Кипре видны звезды, которых нет в северных областях". Это явление можно объяснить только тем, что люди смотрят на звезды с круглой поверхности, продолжил Аристотель, утверждая, что сфера Земли "не имеет больших размеров, ибо в противном случае эффект столь незначительного изменения места не был бы быстро заметен".
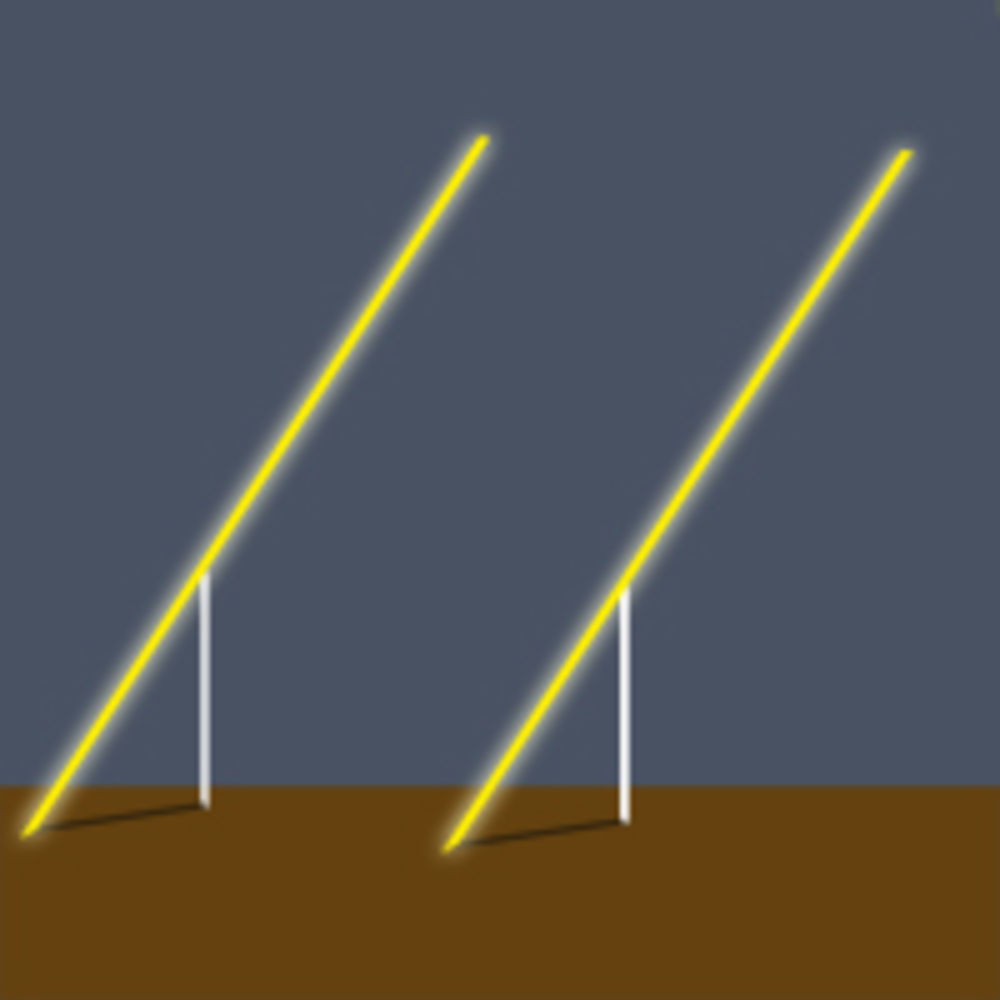
4. Тени и палочки
Если воткнуть палку в землю, она создаст тень. Тень движется с течением времени (таков принцип древних Солнечных часов). Если бы мир был плоским, то две палочки в разных местах породили бы одну и ту же тень:
Но они этого не делают. Это потому, что Земля круглая, а не плоская:
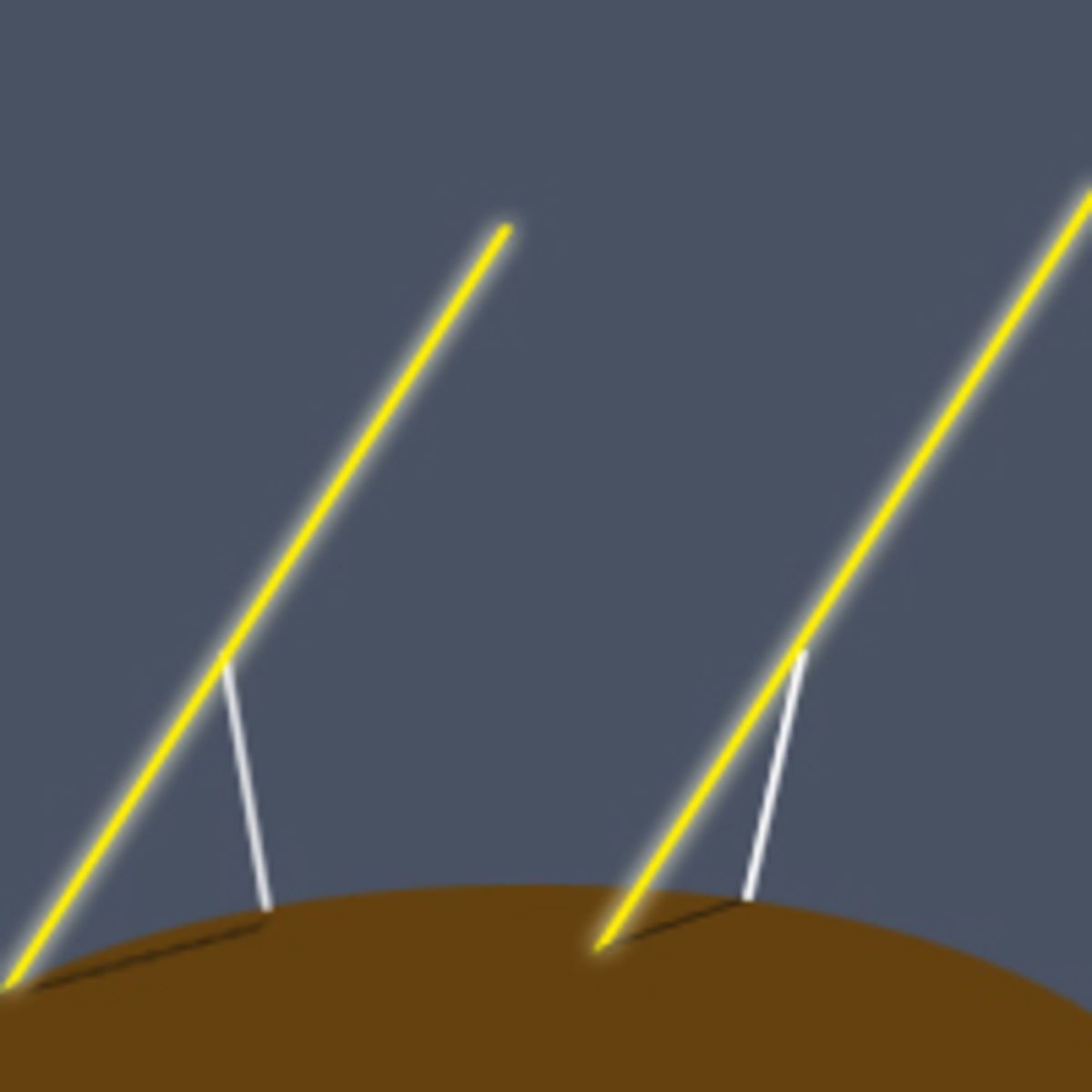
Эратосфен (276-194 гг. до н.э.) использовал этот принцип для достаточно точного вычисления окружности Земли.
5. Вычисления по кривизне Земли
Стоя на плоском плато, вы смотрите вперед, на горизонт. Вы напрягаете глаза, затем достаете свой любимый бинокль и смотрите через него, насколько могут видеть ваши глаза (с помощью линз бинокля).
Затем заберитесь на ближайшее дерево - чем выше, тем лучше, только будьте осторожны, чтобы не уронить бинокль и не сломать линзы. Затем посмотрите еще раз, напрягите глаза и посмотрите в бинокль на горизонт.
Чем выше поднимешься, тем дальше увидишь. Обычно мы склонны связывать это с земными препятствиями - например, с тем фактом, что у нас есть дома или другие деревья, которые мешают нашему обзору на земле, и, поднимаясь вверх, мы получаем четкий обзор, но это не настоящая причина. Даже если бы вы стояли на совершенно чистом плато без препятствий между вами и горизонтом, вы бы видели намного дальше с большей высоты, чем на земле.
Это явление также вызвано кривизной Земли и не произошло бы, если бы Земля была плоской:
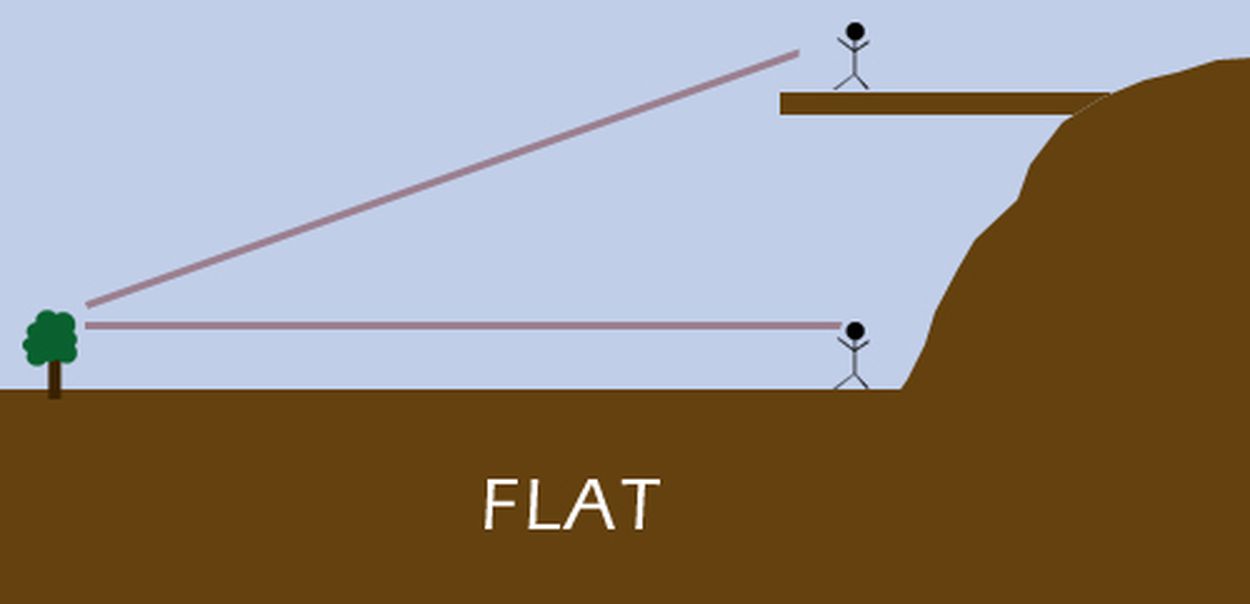

Как далеко вы можете видеть с высоты? На круглой Земле высота имеет большое значение.
6. Полет на самолете
Если вы когда-нибудь выезжали за пределы страны, а именно, на дальние расстояния, вы могли бы заметить два интересных факта о самолетах и Земле:
- Самолеты могут путешествовать по относительно прямой линии в течение очень долгого времени и не падать ни с каких краев. Они также могут совершать кругосветное путешествие по Земле без остановок.
- Если в трансатлантическом полете посмотреть в окно, то в большинстве случаев можно увидеть кривизну Земли на горизонте. Лучший вид кривизны раньше был на Конкорде, но этого самолета давно нет.
7. Посмотрите на другие планеты
Земля отличается от других планет, это правда. В конце концов, у нас есть жизнь, и мы не нашли других планет с жизнью (пока). Однако, есть определенные характеристики, которые есть у всех планет, и будет вполне логично предположить, что если все планеты ведут себя определенным образом, или проявляют определенные характеристики - особенно если эти планеты находятся в разных местах или были созданы при разных обстоятельствах - то наша планета такая же.
Другими словами: если так много планет, которые были созданы в разных местах и при разных обстоятельствах, демонстрируют одно и то же свойство, вполне вероятно, что наша собственная планета также имеет то же свойство. Все наши наблюдения показывают, что другие планеты имеют сферическую форму (и, поскольку мы знаем, как они созданы, также очевидно, почему они принимают такую форму). Если у нас нет очень веских причин думать иначе (чего у нас нет), наша планета, скорее всего, такая же.
В 1610 году Галилео Галилей наблюдал, как спутники Юпитера вращаются вокруг него. Он описал их как маленькие планеты, вращающиеся вокруг большой планеты - описание (и наблюдение), которое было очень трудно принять для церкви, так как оно бросало вызов геоцентрической модели, где все должно было вращаться вокруг Земли. Это наблюдение также показало, что все планеты (Юпитер, Нептун, а позже и Венера) являются сферическими, и все они вращаются вокруг Солнца.
Плоская планета (наша или любая другая планета) была бы настолько невероятным наблюдением, что это противоречило бы всему, что мы знаем о том, как планеты формируются и ведут себя. Это изменило бы не только все, что мы знаем о формировании планет, но и о формировании звезд (нашему Солнцу пришлось бы вести себя совсем по-другому, чтобы приспособиться к теории плоской Земли) и что мы знаем о скоростях и движениях в космосе (как орбиты планет и эффекты гравитации). Короче говоря, мы не просто подозреваем, что наша планета сферическая. Мы это знаем.
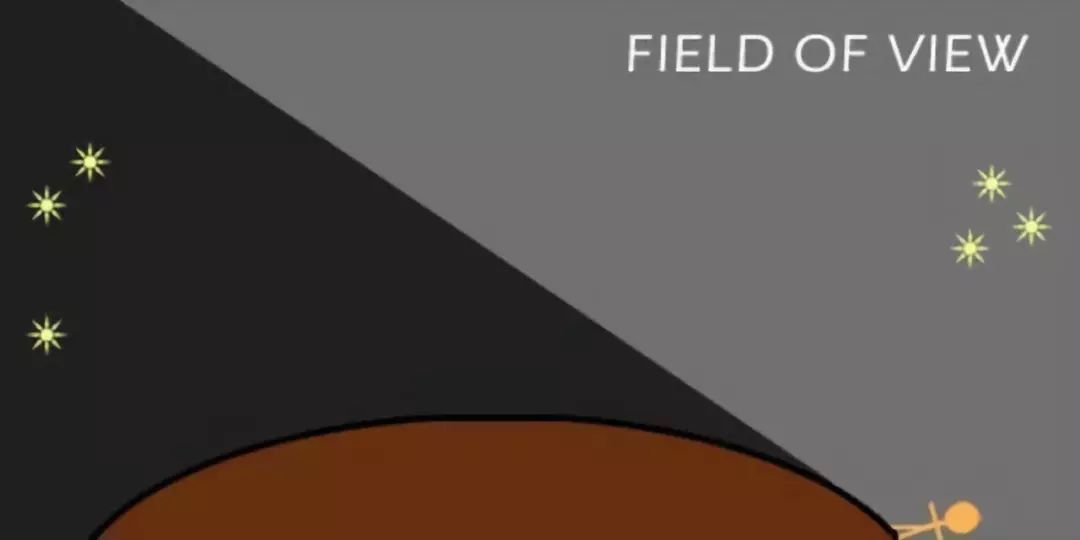
8. Существование часовых поясов

Это можно объяснить только в том случае, если мир круглый и вращается вокруг своей оси. В определенный момент, когда солнце светит на одной части Земли, противоположная сторона становится темной, и наоборот. Это позволяет учитывать разницу во времени и часовые пояса, особенно те, которые превышают 12 часов.
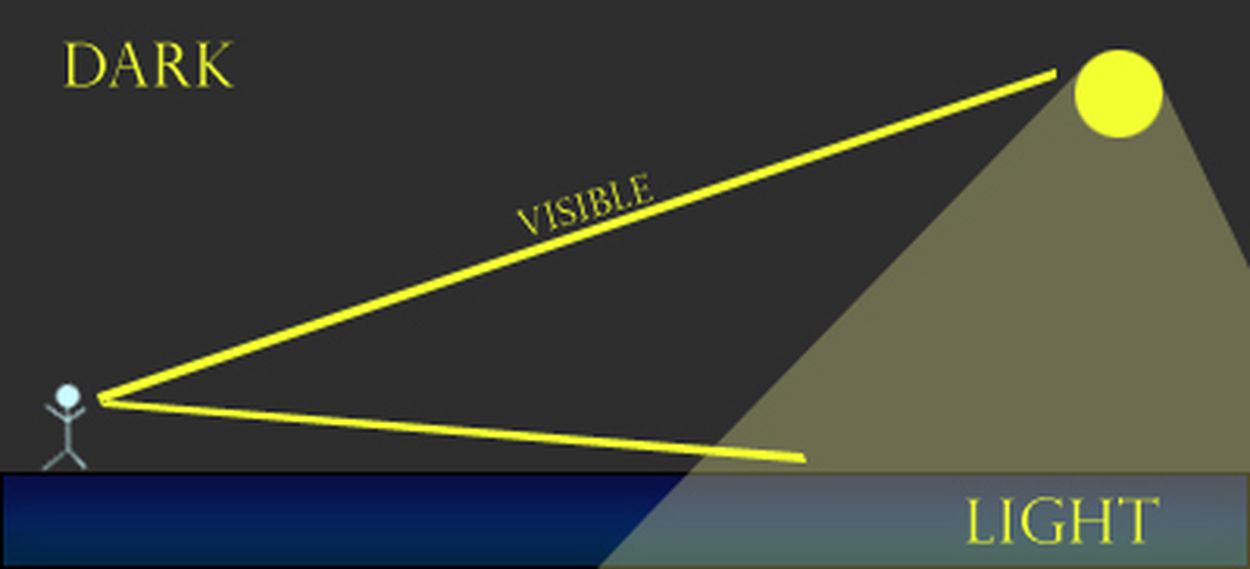
Другая точка, касающаяся часовых поясов, Солнца и Земли: если бы Солнце было "прожектором" (направленным таким образом, чтобы свет падал только на определенное место) и мир был бы плоским, мы бы увидели Солнце, даже если бы оно не светило на нас сверху (как видно на рисунке ниже). Точно так же вы можете видеть свет, исходящий от прожектора на сцене в театре, даже если вы - толпа - сидите в темноте. Единственный способ создать два четко разделенных часовых пояса, где в одном полная темнота, а в другом свет, - это сферический мир.
9. Земное притяжение
Вот интересный факт о мессе: Она притягивает к себе вещи. Сила притяжения (гравитации) между двумя объектами зависит от их массы и расстояния между ними. Проще говоря, гравитация будет притягиваться к центру масс объектов. Чтобы найти центр масс, нужно изучить объект.
Рассмотрим сферу. Так как сфера имеет одинаковую форму, независимо от того, где на ней вы стоите, под вами находится точно такое же количество сферы. (Представьте муравья, разгуливающего по хрустальному шару. С точки зрения насекомого, единственным признаком движения муравья будет то, что он двигает ногами - форма поверхности не изменится вовсе). Центр массы сферы находится в центре сферы, а это значит, что гравитация будет тянуть что угодно на поверхности сферы прямо вниз по направлению к центру сферы. Это произойдет независимо от того, где на поверхности находится объект.

Рассмотрим плоскую плоскость. Центр массы плоской плоскости находится в ее центре, поэтому сила тяжести будет тянуть что угодно на поверхности по направлению к центру плоскости. Это означает, что если вы стоите на краю плоскости, сила тяжести будет тянуть вас в сторону к середине плоскости, а не прямо вниз, как вы обычно испытываете, когда вы стоите на Земле.
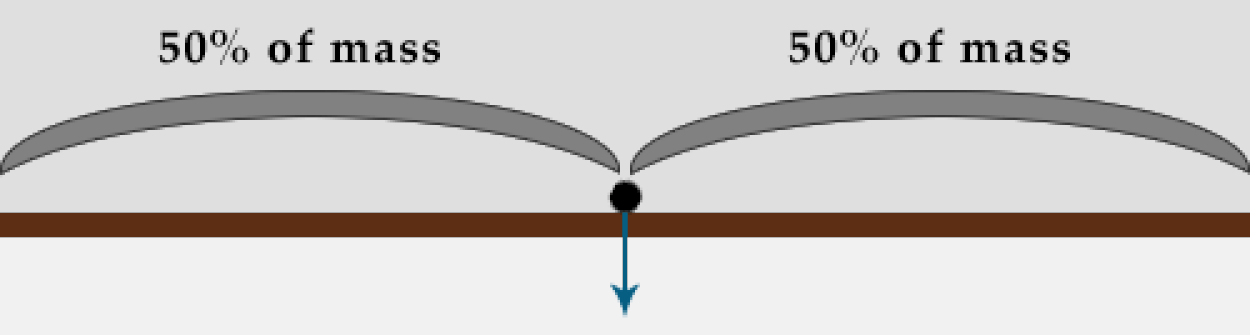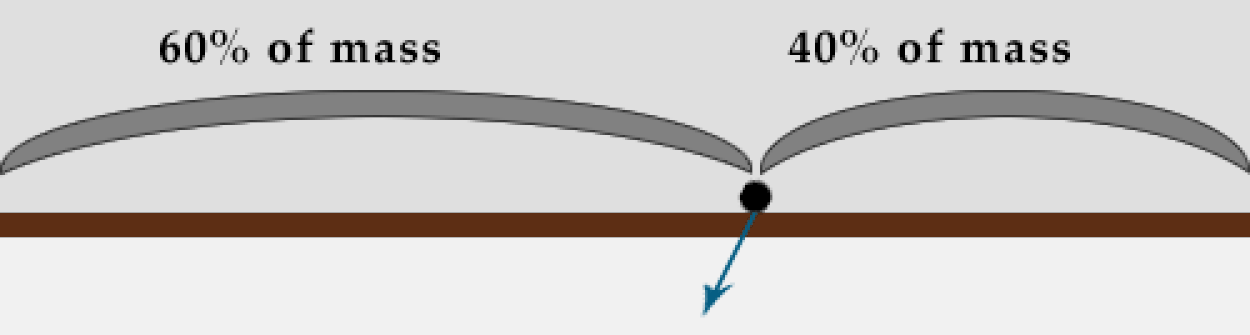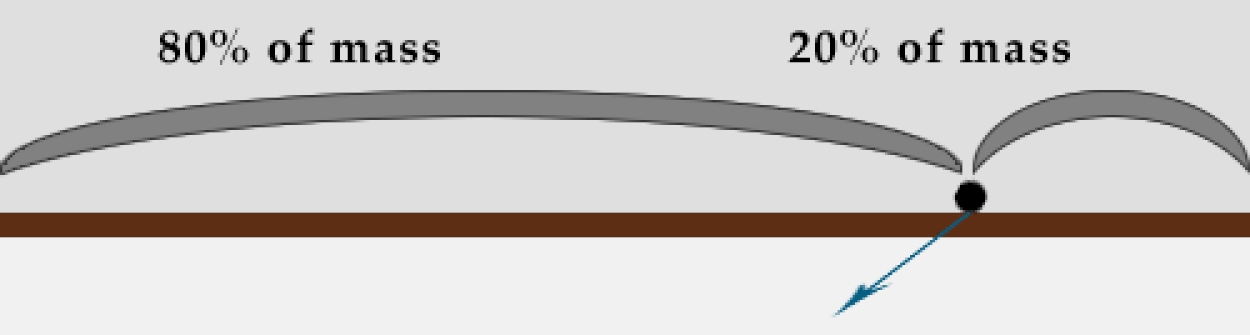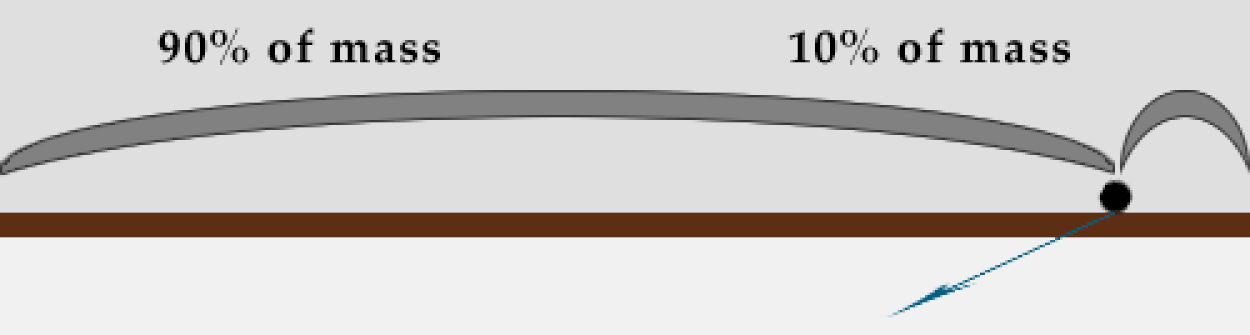
Мы совершенно уверены, что даже у австралийцев яблоко падает вниз, а не боком. Но если у вас есть сомнения, то призываем вас попробовать что-нибудь уронить - просто убедитесь, что это ничего не может сломать или поранить вас.
10. Изображения из космоса
За последние 60 лет освоения космоса мы запустили в космос спутники, зонды и людей. Некоторые из них вернулись, некоторые аппараты до сих пор плавают по Солнечной системе (и почти за ее пределами), и многие передают удивительные снимки на наши приемники на Земле. На всех этих снимках Земля (подождите) сферическая. Искривление Земли видно и на многих, многих, многих фотографиях, сделанных космонавтами на борту Международной космической станции.

Иногда увидеть - значит поверить, и собственное исследование может быть лучшим доказательством, будь то время, потраченное на собственное расследование, или просто поиск результатов других, которые проводили свои собственные эксперименты.