ИИ помогает математикам построить «периодическую таблицу форм»

Столкнувшись со сложностью классификации элементарных геометрических форм, исследователи предложили инновационный подход: создать "периодическую таблицу форм", аналогичную таблице химических элементов. В последних исследованиях для решения этой задачи успешно используется искусственный интеллект с его возможностями быстрого обучения.

Геометрия — фундаментальная основа математики — всегда стремилась расшифровать и классифицировать формы, которые нас окружают. В настоящее время эта дисциплина, как и многие другие, переживает подъем производительности благодаря вмешательству искусственного интеллекта.

Исследователи из Имперского колледжа Лондона и Ноттингемского университета намерены создать "периодическую таблицу форм", подобную таблице химических элементов. Такая таблица позволит классифицировать и лучше понять некоторые из самых элементарных форм, включая "атомарные формы", которые не поддаются дальнейшему разложению. Их работа опубликована в журнале Nature Communications.

Многообразия Фано: неделимые формы

Многообразия Фано — это особая категория геометрических форм, отличающихся принципиальной простотой. Подобно атомам, которые являются базовыми единицами материи и не могут быть разделены на более элементарные частицы, эти многообразия являются элементарными строительными блоками геометрии. Они имеют внутреннюю структуру, которая не позволяет разложить их на части.

Однако, несмотря на кажущуюся простоту, многообразия Фано имеют скрытую сложность, которая представляет собой настоящую головную боль для математиков. Их классификация требует глубокого понимания их свойств и взаимосвязи между собой. Подобно тому, как химикам пришлось детально изучать свойства атомов, чтобы составить периодическую таблицу элементов, математикам предстоит решить сложную задачу классификации этих первичных форм.

Эта задача тем более сложна, что, в отличие от атомов, которые можно наблюдать и изучать с помощью таких приборов, как электронные микроскопы, многообразия Фано являются чисто математическими сущностями. Поэтому для их изучения требуются инструменты и методы, характерные для геометрии, а также концептуальный подход, позволяющий понять их сущность.

Квантовый период: уникальный "отпечаток пальца" для многообразий Фано

Каждое многообразие Фано имеет свою характеристику, называемую "квантовым периодом", поясняют авторы в пресс-релизе. Эта числовая последовательность играет роль, аналогичную роли штрих-кода или отпечатка пальца для объекта или человека: она позволяет однозначно идентифицировать данную разновидность. Хотя исследователи и предполагали, что этот квантовый период может определять размерность многообразия Фано, точный механизм, лежащий в основе этой связи, до сих пор оставался загадочным. В отсутствие надежной теории по этому вопросу было трудно подтвердить эту гипотезу на всех выявленных многообразиях Фано.

Именно здесь на помощь приходит машинное обучение — направление искусственного интеллекта. Эти алгоритмы специально разработаны для выявления тенденций и закономерностей в больших массивах данных. Предоставив модели машинного обучения выборку данных о разновидностях Фано и периодах их квантования, исследовательская группа смогла обучить модель распознавать и предсказывать взаимосвязи между этими разновидностями. Результаты оказались впечатляющими: обученная модель смогла предсказать размерность многообразий Фано только на основе их квантовых периодов с удивительной надежностью 99%.

Взаимодействие ИИ и математики: "благотворный симбиоз"

Подход, использованный исследовательской группой, является прекрасной иллюстрацией взаимодополняемости традиционных методов и современных инструментов. Хотя модель ИИ позволила получить ценные сведения о связи между квантовым периодом и размерностью многообразий Фано, ее одной было недостаточно для формального доказательства. Поэтому исследователи объединили предсказания ИИ с проверенными математическими методами для подтверждения этой связи, используя ИИ в качестве компаса для проведения своих исследований.

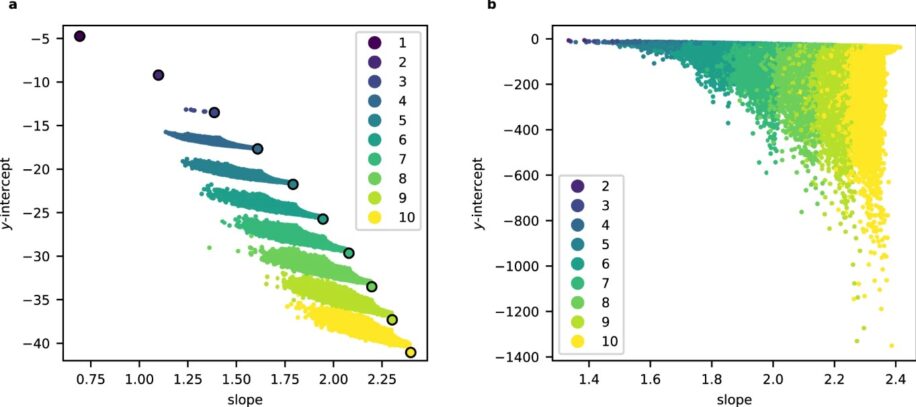
Не ограничиваясь этим конкретным применением, команда подчеркнула важность математических данных для разработки и совершенствования моделей машинного обучения. В отличие от реальных данных, которые зачастую омрачены неровностями и шумами, математические данные обладают непревзойденной ясностью и точностью. Они лишены случайных помех, которые могут запутать модели.

Профессор Том Коут, сотрудник кафедры математики Имперского колледжа Лондона, подводит итог: "Искусственный интеллект может произвести настоящую революцию в математике, поскольку мы показали, что машинное обучение является мощным инструментом для выявления закономерностей в таких сложных областях, как алгебра и геометрия.

Подвергая их воздействию "чистых" данных, исследователи могут улучшить способность моделей распознавать и интерпретировать сложные закономерности. Подобно тому, как периодическая таблица элементов произвела революцию в химии, периодическая таблица форм может изменить наше понимание геометрических фигур. Она также может проложить путь к новым открытиям в физике, биологии и других отраслях науки.