Есть ли что-нибудь более сложное, чем комплексные числа?
В математике существует несколько систем чисел, более сложных, чем комплексные числа, например, кватернионы.
Когда мы были детьми, единственные числа, которые нас волновали, были те, которые нужны для счета. Сколько у тебя глаз? Два! Сколько тебе лет? Семь! Сколько конфет ты хочешь? Ну... бесчисленное множество, но суть вы уловили.
Нам не нужны были другие числа, кроме тех, которые использовались для подсчета вещей, потому что они естественным образом появлялись в природе, и так родились натуральные числа.
По мере того как вы взрослели и проваливали все больше и больше тестов, вы поняли важность нуля. В итоге вы добавили этот ноль к существующему набору чисел и получили целые числа.
Все становилось все сложнее. В какой-то момент вы встретили в жизни отрицательных людей, которые познакомили вас с концепцией отрицательных целых чисел.
Были также рациональные и иррациональные люди, которые обрушили на вас бомбардировку из совершенно странных видов чисел.
Однако все это было в порядке вещей, потому что вы знали, что все они реальны, но счастье было недолгим. Числа так сильно зацепили вас, что вскоре вы уже представляли их себе. Вы просто не могли за ними угнаться, потому что они становились все сложнее, и в конце концов вы просто сели и задумались: "Неужели это когда-нибудь закончится?
Эти сложные числа кажутся довольно сложными, верно? Можно ли на этом остановиться или есть что-то еще более сложное, чем комплексные числа?".
Спойлер: да, есть кое-что еще более сложное... и оно оказывается еще хуже.
Что такое комплексные числа?
Давайте сначала рассмотрим мнимые числа. Что такое мнимое число и что делает его мнимым? Прежде всего, мнимые числа не входят в набор действительных чисел. К действительным числам относятся все целые числа, а также рациональные и иррациональные числа.
Вам может показаться, что действительные числа содержат все числа, но это не совсем так. Подумайте вот о чем: каков квадратный корень из 4? Вы ведь знаете ответ на этот вопрос, верно? Это либо 2, либо -2 (потому что оба числа при умножении на себя дают одно и то же число).
Довольно просто, верно? А теперь попробуйте спросить, каков квадратный корень из -4? Давайте подумаем об этом. Какое число при умножении на себя дает -4? Ответ не может быть 2 или -2, потому что их нужно умножать друг на друга, а не на самих себя (так как 2 и -2 - это два совершенно разных числа).
В такие моменты мы используем мнимое число i. Значение i равно √ - 1 (получается i2 = - 1). Таким образом, мы можем написать, что квадратный корень из -4 равен 2i. Любое число в паре с i становится мнимым числом.
Комплексное число - это комбинация действительного и мнимого чисел. Оно имеет вид:
Комплексное число = действительное число + мнимое число
Например, мы можем иметь комплексное число 4+3i, где 4 - действительная часть, а 3i - мнимая часть.
Как комплексные числа "вращаются"?
Давайте сначала представим эти числа на графике. С самого детства нас учили числовой линии. Числовая линия может показать все действительные числа от ∞ до ∞.
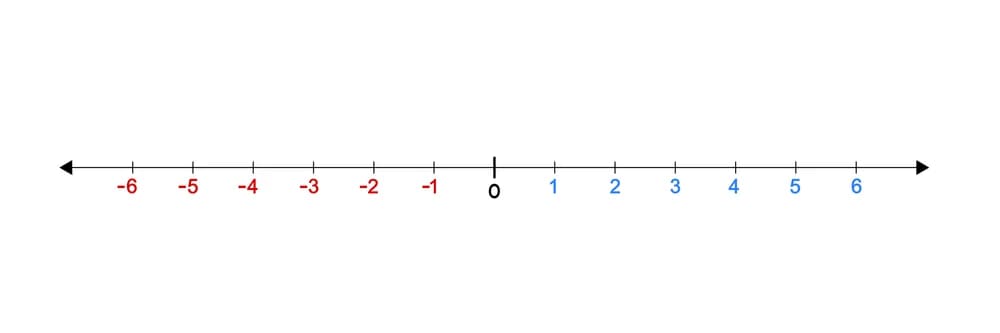
Видите ли, линия является одномерной, поэтому для представления действительных чисел вам нужно только одно измерение. Можно также сказать, что действительные числа одномерны.
Теперь давайте посмотрим, как можно представить комплексные числа. Как упоминалось ранее, комплексные числа состоят из двух частей - действительной и мнимой, поэтому для их графического представления нам нужны две линии: одна линия для действительной части, как и раньше, и одна линия для мнимой части, в единицах i.
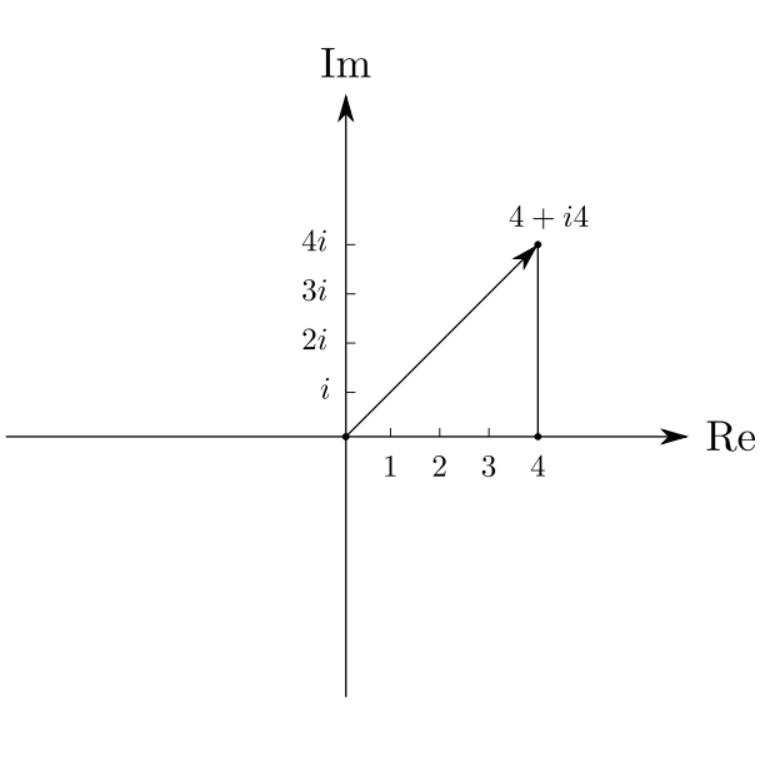
Итак, комплексные числа нуждаются в двух линиях или осях для графического представления, поэтому они двумерны, и есть одна очень интересная вещь, которую можно делать в двух измерениях... вращать!
По прямой линии мы можем двигаться только вперед или назад, но в двухмерной плоскости мы можем двигаться вверх-вниз, влево-вправо или даже двигаться по полному кругу, вращаясь на 360 градусов.
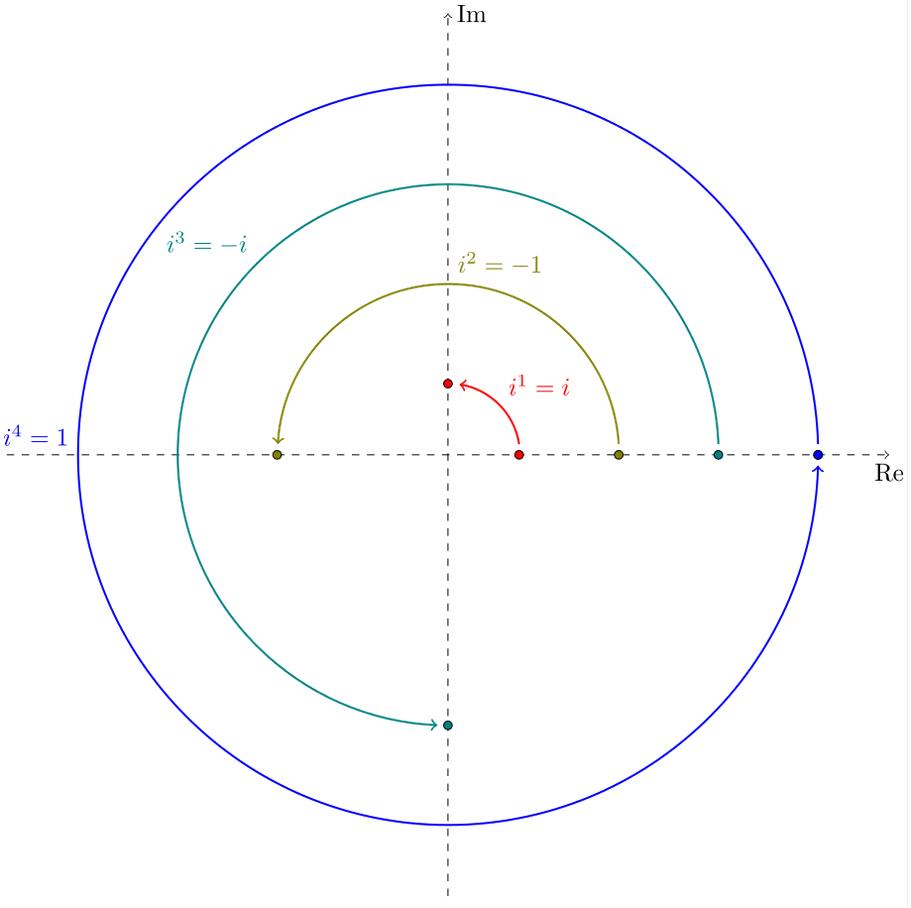
Мы можем двигаться по горизонтальной оси, складывая или вычитая действительное число, и можем двигаться по вертикальной линии, складывая или вычитая мнимое число, но если мы умножаем комплексное число на i, то в итоге мы поворачиваем число (это все равно что выбрать число и переместить его по периметру круга, а затем поместить под другим углом) на определенный угол.
Так как же вращать в трех измерениях?
Именно этот вопрос беспокоил Уильяма Гамильтона во время прогулки с женой. Его осенило внезапное осознание того, что проблему решит четырехмерное число.

Считается, что он вырезал первое правило своих новых четырехмерных чисел, известных как кватернионы, прямо на мосту Броуэм:
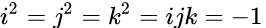
Это очень похоже на правило i2 = - 1 для мнимых чисел.
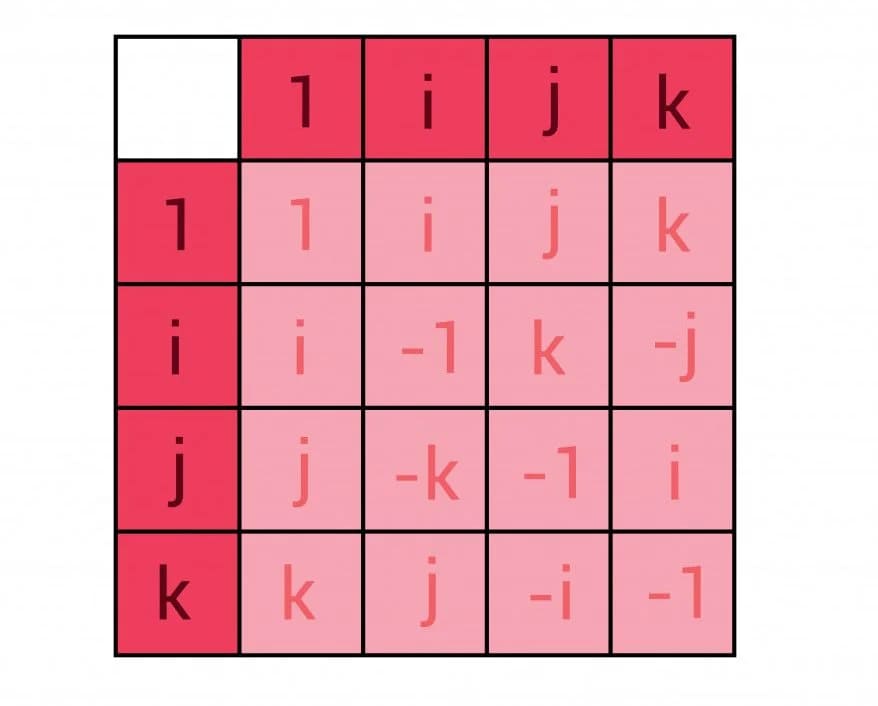
Как и комплексные числа, кватернион записывается как комбинация этих чисел вместе с действительным числом, например: 6+2i+4j+7k.
Как мы видели в двумерном случае комплексных чисел, умножение на i поворачивает число в двумерной плоскости; в случае кватернионов умножение на любое из i, j, k или их комбинаций поворачивает число в трех измерениях.
Это чрезвычайно важное свойство кватернионов, которое используется в графическом программировании для того, чтобы заставить анимированные объекты вращаться в окружающей среде. Фактически, кватернионы также используются для отображения и программирования вращения ваших смартфонов и планшетов.
Итак, да, существуют более сложные системы чисел, чем комплексные числа, одну из которых мы видели здесь в виде кватернионов - 4-мерных чисел. Существуют даже системы 8-мерных и 16-мерных чисел, но они не очень полезны и поэтому практически не обсуждаются (даже в кругах любителей математики).