Что такое тессеракт? Четырехмерный объект, который невозможно построить

Тессеракт - это четырехмерный гиперкуб с 24 гранями, 32 ребрами и 16 вершинами. Он может быть создан путем утолщения куба в четвертом измерении. Хотя тессеракт невозможно построить физически, мы можем визуализировать его в нашем трехмерном мире.
Идея четвертого пространственного измерения манила людей с момента ее появления. В физике три измерения представляют собой пространство (x,y,z), а четвертое измерение - время (t). Однако в абстрактной математической концепции может существовать бесконечное число пространственных измерений.
Давайте попробуем понять четвертое измерение. В геометрии четырехмерный аналог куба называется тессерактом. Его легко экстраполировать, рассматривая более низкие измерения.
- Нульмерный куб - это точка, вершина.
- Одномерный куб - это отрезок прямой с 2 вершинами (по одной на каждом конце). Его можно создать путем увеличения толщины точки в одном измерении.
- Двумерный куб - это квадрат с 4 вершинами. Его можно создать, увеличив толщину отрезка линии во втором измерении.
- Трехмерный куб - это куб с 8 вершинами, созданный путем увеличения толщины квадрата в третьем измерении.
Аналогично, четырехмерный куб (также известный как гиперкуб или тессеракт) имеет 16 вершин. Он может быть создан путем сгущения куба в четвертом измерении. Но поскольку мы живем в трехмерном мире, построить четырехмерный объект невозможно.
В целом можно сказать, что тессеракт относится к кубу так же, как куб относится к квадрату. У него 24 грани, 32 ребра и 16 вершин.

Тессеракт очень трудно визуализировать
Визуализировать тессеракт или любой другой четырехмерный объект чрезвычайно трудно, если вообще возможно. Это происходит потому, что наше воображение недостаточно сильно, чтобы спроецировать наше сознание в искусственный мир, который сильно отличается от нашего собственного.
Наш мозг устроен так, чтобы преобразовывать двухмерные данные в трехмерное представление. Точнее, наши глаза посылают в мозг пару двухмерных изображений, из которых мозг строит двухмерную+глубинную модель поля зрения.
Это то, о чем наш мозг лучше всего приспособлен думать. Трехмерное пространство легко визуализировать, потому что мы буквально видим его все время. Однако у нас нет прямого опыта более высоких измерений, и поэтому у людей нет четкого прототипа, который можно было бы использовать в качестве трамплина для их визуализации.
С другой стороны, физики и математики, имеющие опыт работы с более высокоразмерными пространствами, более способны, чем остальные, визуализировать их в своем мозгу.
Давайте попробуем визуализировать тессеракт
Как куб можно спроецировать в двухмерное пространство, так и тессеракт можно спроецировать в трехмерное пространство.
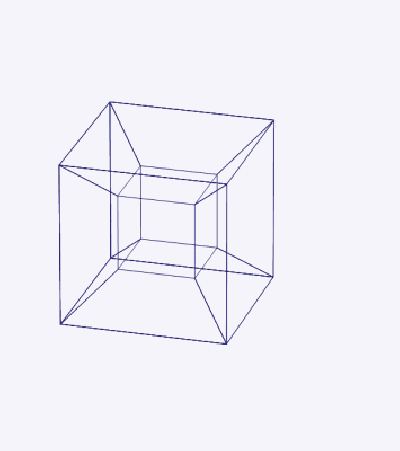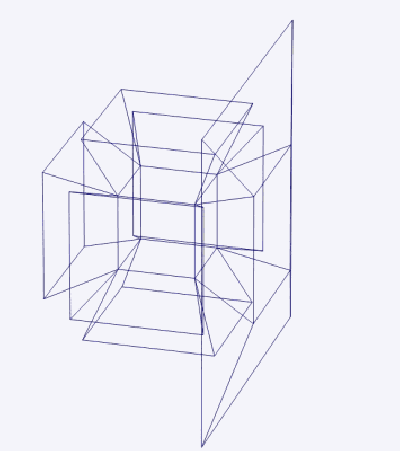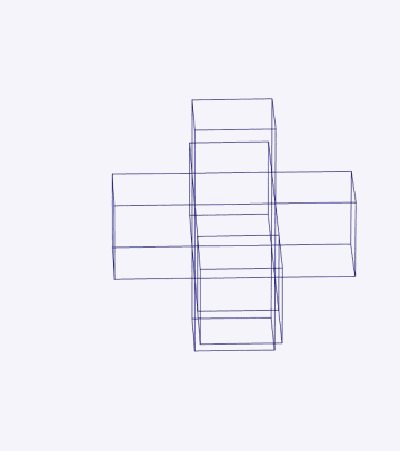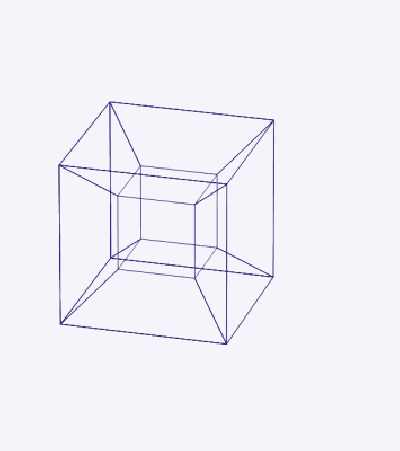
Поверхность трехмерного куба содержит 6 квадратных граней; аналогично гиперповерхность тессеракта содержит 8 кубических ячеек.
Тессеракт можно развернуть на 8 кубиков в трехмерном пространстве (рис. 2). Это похоже на развертывание куба на 6 квадратов в двумерном пространстве. Разворачивание геометрического объекта [с плоскими сторонами] называется сеткой. В тессеракте 261 сетка.
Существует два типа четырехмерных вращений:
1) Простые вращения: трехмерная проекция Тессеракта (рис. 3), выполняющая простое вращение вокруг плоскости, разделяющей пополам фигуру сверху вниз и спереди слева направо.

2) Двойное вращение: трехмерная проекция тессеракта (рис. 4), показывающая двойное вращение вокруг двух ортогональных плоскостей.

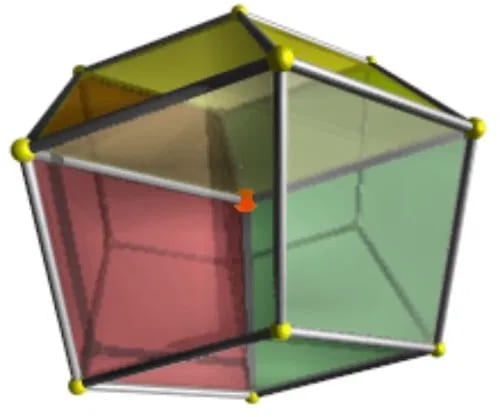
Тессеракт также может быть показан с точки зрения устранения скрытого объема. На рисунке 5, например, красная грань находится ближе всего к четвертому измерению и имеет четыре кубические ячейки, расположенные вокруг нее.
Тессеракт был открыт в 1888 году
Слово "тессеракт" было придумано британским математиком и писателем-фантастом Чарльзом Говардом Хинтоном. Он впервые использовал это слово в 1888 году в своей книге "Новая эра мышления". Он также придумал несколько новых слов для описания элементов в четвертом измерении.
С тех пор слово "тессеракт" используется в различных видах искусства, архитектуры и научно-фантастических историях (таких, как "Мстители" и "Агенты «Щ.И.Т.»"), где оно не имеет ничего общего с четырехмерным гиперкубом.
Последние исследования
Пространственные представления человека не ограничены трехмерным миром
Группа исследователей из Университета Иллинойса, США, провела исследование, чтобы выяснить, может ли человек развить интуитивное понимание четырехмерного пространства. Для получения точных результатов они использовали виртуальную реальность (VR).
Данные показывают, что люди, не имеющие специальной практики, могут научиться делать пространственные суждения о длине и угле между линейными сегментами, встроенными в четырехмерное пространство, просматриваемое в виртуальной реальности. Их суждение включало данные как трехмерной проекции, так и четвертого измерения. Основные представления были основаны на визуальных образах (установленных алгебраической природы), хотя и примитивных и недолговечных.
Общее число возможных измерений во Вселенной
В то время как общая теория относительности рисует картину четырехмерной Вселенной, теория суперструн утверждает, что она имеет 10 измерений, а расширенная версия, называемая М-теорией, утверждает, что она имеет 11 измерений. В бозонической теории струн пространственное время 26-мерно. Эти теории просто представляют собой математические уравнения. Они настолько сложны, что никто не знает их точной формы.
Эксперимент по изучению теоретических материалов в четырехмерном пространстве
Международная группа исследователей смогла разработать двумерную экспериментальную систему, которая позволяет им анализировать физические свойства "материалов", которые теоретически существуют только в четырехмерном пространстве.
Более конкретно, они продемонстрировали, что четырехмерные квантовые эффекты Холла могут быть эмулированы с помощью фотонов, проходящих через двумерный волноводный массив.
Как эти исследования могут быть полезны в нашем трехмерном мире? Скажем, квазикристаллы (широко используемые для покрытия некоторых антипригарных сковородок), как было показано, имеют скрытые измерения. Этот эксперимент может помочь нам понять физику этого скрытого измерения. Затем эта физика может быть использована в качестве принципа проектирования нового фотонного оборудования.